JUMP TO TOPIC
Factors of 6: Prime Factorization, Methods, Tree, and Examples
Factors of 6 are the numbers that can equally divide the number 6 while producing a whole number quotient and zero remainders. If these numbers are multiplied by each other, they will also result in the number 6. As 6 is a composite number it will have more than 2 factors.
Figure 1 – All possible Factors of 6
What Are the Factors of 6?
Factors of 6 are 1, 2, 3, and 6. These numbers can divide evenly to form 6 and multiply together to form the number 6.The number 6 is small so if we look into its factors we can get the following list:Factors of 6 = 1, 2, 3, 6
How To Calculate the Factors of 6?
We have 2 different ways to calculate the factors of the following number, which are Division Method and Multiplication Method.In the Division method, we take the original number, 6, as the numerator and divide it by every consecutive integer in the number line. We start with the smallest integer 1 and end at 6. We will calculate all of the factors by following these steps:\[ \dfrac{6}{1}=6 \]The remainder is zero.\[ \dfrac{6}{2}=3 \]\[ \dfrac{6}{3}=2 \]\[ \dfrac{6}{6}=1 \]The above-given numbers are considered as the factors of 6 because when divided they give zero remainders and a whole number quotient.Similarly, if 2 numbers are multiplied to give 6 then both the multiplier and multiplicand will be considered as the factors of that number. We can find the factors of 6 by multiplication method in the following way:1 x 6 = 6
2 x 3 = 6
In these steps, all of the factors when multiplied with one another give 6 as an answer. So we can write the factor list of 6 as:Factors of 6 = 1, 2, 3, 6
We can also find the negative factors of 6 by both the division method and multiplication method, so:Negative Factors of 6 = -1, -2, -3, -6
Factors of 6 by Prime Factorization
Prime Factorization of any number is the product of 2 or more prime factors. as we have already discussed that 6 is a composite number which means that it will have some prime factors. To get the prime factorization of the number 6 we will follow these steps:6 $\div$ 2 = 3
We will start by dividing 6 by the smallest prime number which is 2. As the answer is a whole number with zero remainders we will keep on dividing the answer until we get 1 as an answer3 $\div$ 3 = 1
Remainder = 0We can compile this as the product of all prime factors which are:6 = 2 x 3
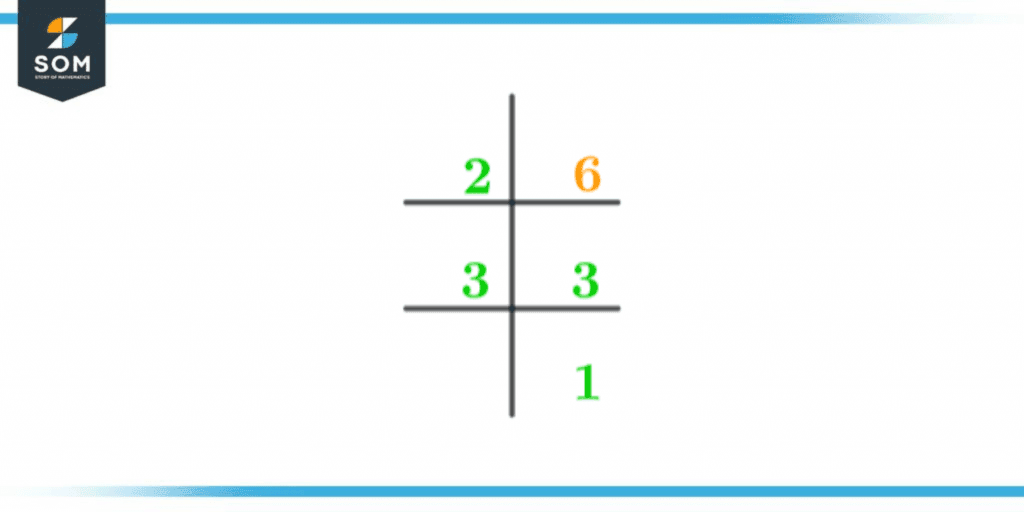
Figure 2 – Prime Factorization of 6
Factor Tree of 6
The number 6 has 2 prime factors. We will now demonstrate these factors using a factor tree. A factor tree is like an actual tree consisting of branches. We use this method to pictorially analyze the prime factor of any number by using some logic.The factor tree of 6 is a combination of prime factors which is shown below: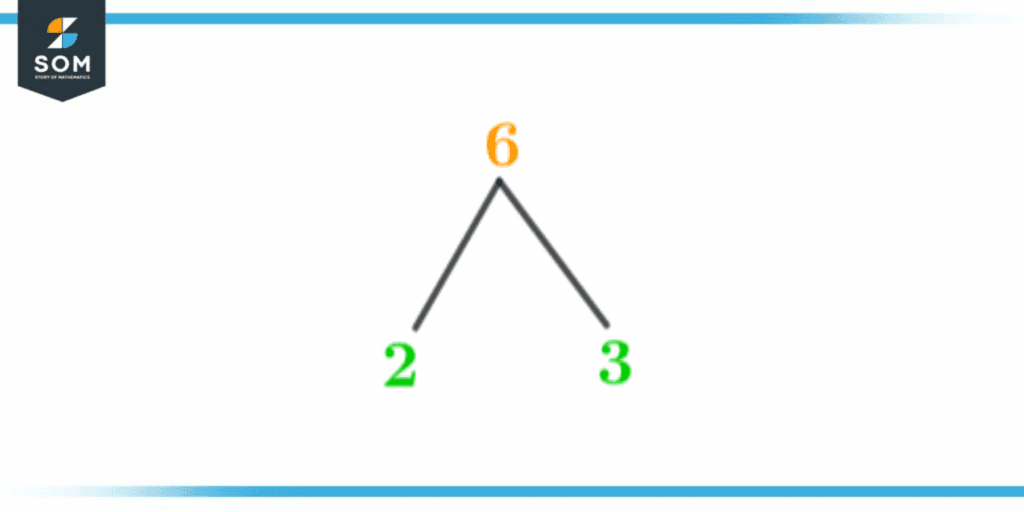
Figure 3 – Factor Tree of 6
Factors of 6 in Pairs
Factor Pair is a set of 2 numbers when multiplied together to give the desired number. Factor pairs of the number 6 can be calculated by multiplying 2 factors. We can use this method to find the number 6. We will take any 2 pairs and will multiply them. If the solution is equal to 6 then the two factors will be considered as factor pairs. The following steps show how to find the factor pair of the number 6:1 x 6 = 6 2 x 3 = 6 3 x 2 = 66 x 1 = 6 When listing the pairs we will not repeat the same factors so the factor pairs are given as:(1,6)(2,3)We know that every number has positive and negative factors similarly, they also have negative pair factors.-1 x -6 = 6 -2 x -3 = 6-3 x -2 = 6-6 x -1 = 6Note that when we multiply two negative numbers the answer will be a positive number. So we can write the negative factor pairs as:(-1,-6)(-2,-3)Factors of 6 Solved Examples
Example 1
Dory wants to find a common factor of 27, 9, and 6. Help her find it.Solution
As we know Factors of 6:Factors of 6 = 1, 2, 3, 6
Similarly, Factors of 9:Factors of 9 = 1, 3, 9
Factors of 27:Factors of 27 = 1, 3, 9, 27
So from the above factors list, we can say that the number 3 is a common factor 6, 9, and 27.Example 2
Zoey wants to know what is the Greatest and Smallest Factors for her math homework. Help Zoey to find the greatest and smallest factor of 6.Solution
As we know the factors of 6 are:Factors of 6 = 1, 2, 3, 6
A factor can never be greater than the number itself nor can be zero. So we can say that:Greatest Factor of 6 = 6
Smallest Factor of 6 = 1
Example 3
James wants to put a 6 feet rug in his lounge. He wants to know what dimensions should he choose to get a rug perfect for his lounge.Solution
As we know:Area= length x width
So if the desired area is 6 so we will look into its factor pairs for the dimensions of the rug.2 x 3 = 6
Hence the rug should have (2,3) dimensions.Example 4
Arya has only 6 chocolates left from Halloween treats. She wants to divide them between her two sisters. How many chocolates will each sister get?Solution
The factors of 6 are:Factors of 6 = 1, 2, 3, 6
From the above list, we can say that 6 chocolates can be equally divided into two parts as 2 is a factor of 6. Hence:\[ \dfrac{6}{2}=3\ ]So each sister will get 3 chocolates.Images/mathematical drawings are created with GeoGebra.
