JUMP TO TOPIC
Factors of 60: Prime Factorization, Methods, Tree, and Examples
Factors of 60 are the numbers that evenly divide 60, leaving the remainders as zero. Factors of a number can be positive as well as negative. Positive and negative factors are the same but have opposite signs.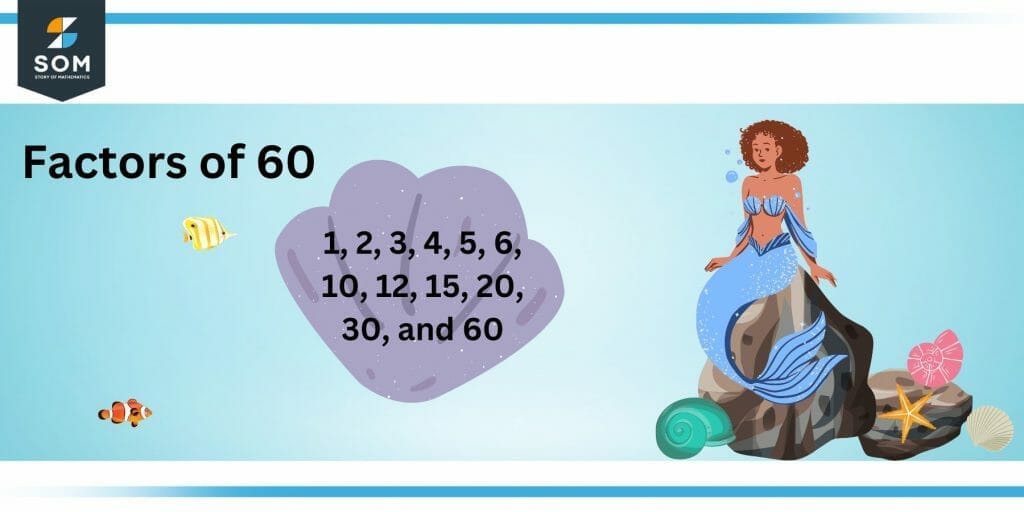
Figure 1 – All factors of 60
What Are the Factors of 60?
The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. Number 60 is evenly divisible by all these integers. 60 has twelve positive factors. By multiplying these integers in such pairs that their result must be equal to 60, those numbers are said to be the factor pairs of 60.How To Calculate the Factors of 60?
You can calculate the factors of 60 by using the division method. The rule we must follow is that the remainder of the division must be zero. There are two most common methods to find the factors of a number.- Division Method.
- Multiplication Method.
- Factors are always whole numbers, and can not be written in p/q form. In other words, factors can never be in the form of fractions or decimals.
- Every integer has a unique prime factorization expression.
- All even numbers have 2 as their factor.
- Every number contains a finite number of factors.
- A factor of a number can never be greater than the number itself.
- A number having more than two factors is known as a composite number.
- If a number has only two factors, the number is a prime number.
Factors of 60 by Prime Factorization
Prime factorization means breaking a composite number into prime numbers that are its factors. By multiplying these prime numbers, if the product is equal to 60, the multiplicands are known as prime factors of 60.The two common ways to find prime factorization are:- Factor Tree.
- Division Method.
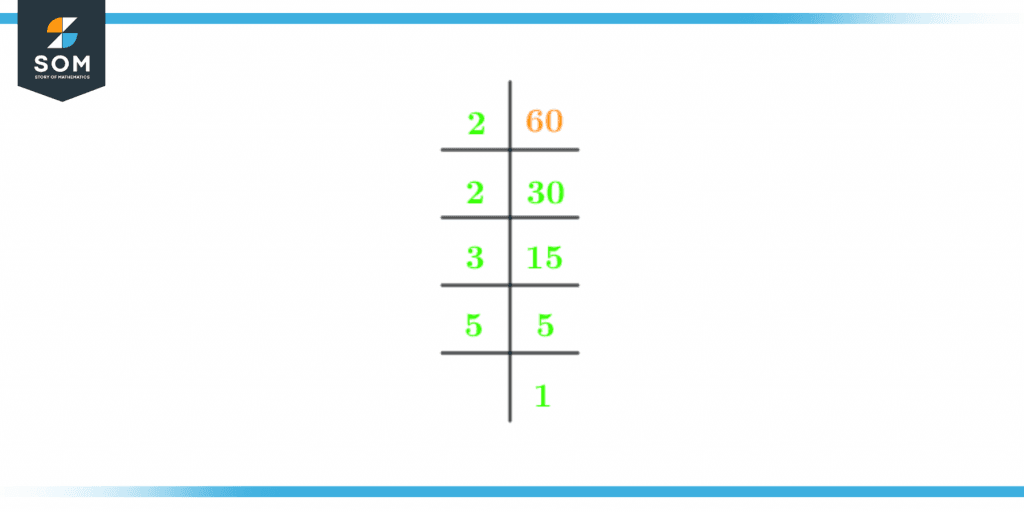
Figure 2 – Prime Factorization of 60
2 x 2 x 3 x 5 = 60
This can also be written as$2^2$ x 3 x 5 = 60
Factor Tree of 60
The factor tree is a special diagram that expresses a number in the form of its prime factors. A factor tree is a pictorial representation.It consists of the number at the top; further, splits into two branches, one consisting of a quotient, and the other one consisting of a devisor. The quotient will be further divided and branched. The process of division goes on until you can’t make further factors. The factor tree of 60 is shown below as: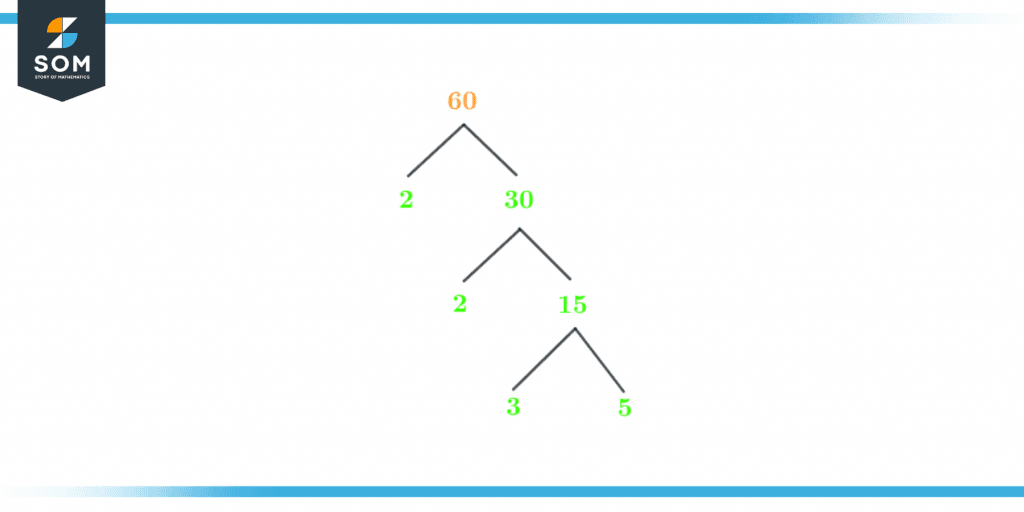
Figure 3 – Factor Tree of 60
Factors of 60 in Pairs
Factor pairs are factors of the given number. We multiply those factors so that their product is equal to the original number. A set of two factors, when multiplied together, gives a particular number that is equal to the original number.Factors when multiplied to give product 60, will be known as factor pairs of 603 x 20= 60
60 is the product of 3 and 20. In other words, 60 is a multiple of 3 and 20. Hence, 3 and 20 are factor pairs of 60.4 x 20= 80
4 and 20 both are factors of 60, but when multiplied the product is not equal to 60. Hence, they are not a factor pair of 60. Positive factor pairs of 60 are as follows:1 x 60= 60
2 x 30= 60
3 x 20= 60
4 x 15= 60
5 x 12= 60
6 x 10= 60
By looking at the above multiplication, we will write the factor pairs for 60 as (1, 60), (2, 30), (3, 20), (4, 15), (5, 12), and (6, 10). Negative factor pairs of 60 are as follows:-1 x -60= 60
-2 x -30= 60
-3 x -20= 60
-4 x -15= 60
-5 x -12= 60
-6 x -10= 60
When a negative sign is multiplied by a negative sign, the product is always positive. The negative factor pairs are (-1, -60), (-2, -30), (-3, -20), (-4, -15), (-5, -12), and (-6, -10),Factors of 60 Solved Examples
For further understanding, here are some solved examples of factors of 60.Example 1
Find the range of factors of 60.Solution
First of all, list the factors of 60. Keep in mind factors should be in ascending orderFactors of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60The formula to calculate the range is as follows:Range = Max Value – Min ValueThe max value means the greatest number in the factors list, and the min value is the lowest number in the factor list.Max value: 60
Min value: 1
Now putting the values in the formula of rangeRange = 60-1
Range = 59
The range for factors of 60 is 59Example 2
Find the common factors of 40 and 60.Solution
Firstly, list the factors of 40 and 60.Factors of 40 are:Factors of 40 = 1, 2, 4, 5, 8, 10, 20, 40Factors of 60 are:Factors of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60Common factors are the factors that are present in both lists of factors. Common factors of 40 and 60 are:Common factors are = 1, 2, 4, 5, 10, 20Example 3
Jony bought 60 candies for his birthday party. The cost of one candy was 2$. Calculate the total cost of 60 candies. He made X number of goodie bags, he placed 5 candies in each goodie bag. Also, calculate how many goodie bags he made.Solution
Cost of one candy = 2
Total candies he bought = 60
The total cost will be:Total cost:2 x 60 =120
Candies in each bag= 5
Total goody bags= X
\[\frac {60}{5}= 12\]Jony made 12 goodie bags for his birthday party.Images/mathematical drawings are created with GeoGebra.