JUMP TO TOPIC
Factors of 68: Prime Factorization, Methods, Tree, and Examples
Factors of 68 is a list of numbers representing the original number 68 when multiplied by each other. This makes them unique in such a way that if we divide 68 by any of these factors, it will always give a whole number quotient.
Figure 1 – All possible Factors of 68
What Are the Factors of 68?
The factors of 68 are 1, 2, 4, 17, 34, and 68. 68 is a composite number which is why it has more than two factors. The number 68 has a total of 6 elements.In total, 68 has a capacity of 6 factors, which can be grouped into 3-factor pairs. They can be positive and negative.How To Calculate the Factors of 68?
The factors of 68 can be calculated using methods of division. Along with division, another way of prime factorization can be used to find only the prime factors of 68. This prime factorization can also be represented visually through a factor tree diagram.Division
Factors of any number are specific numbers that give a remainder equivalent to zero and a whole number quotient. For any number to be a factor of 68, the quotient it produces must be a number with no decimals.One of the methods, called the division method, is a way to find out these factors of 68; this method is entirely a technique based on the mathematical operation of division. We start by dividing the given number, such as 68, by numbers that we think might be divisible. Parsing through the results and ignoring the numbers that produce a decimal quotient usually gets us to our answer. Below is the complete division method to find out the factors of 68:Step 1: In the first step, we write down the number 68 and identify whether it’s an even number or an odd number. For any even number, we know that they are always divisible by two, but for odd numbers, we start from and check whether it is divisible by 3. As 68 is even, we know now that it will be divisible by two as all even numbers are divisible by 2:\[ \frac{68}{ 2} = 34 \]As 34 is the quotient in this division and it is a whole number, 2 is a factor of 68.Step 2: Now we find the next factor; we know that 68 is not divisible by three, so we try four instead, now 68 is also divisible by 4, so 4 is a factor too:\[ \frac{68}{ 4} = 17 \]Step 3: The next number we verify as the factor of 68 is 17 because no other number that divides 68 into a whole number and gives a zero remainder:\[ \frac{68}{ 17} = 4 \]Hence 17 is also a factor of 68.Step 4: From step 1, we can see that 2 divides 68 without any remainder with the quotient 34, so we will try 34 as well:\[ \frac{68}{ 34 }= 2 \]As 2 is a whole number, it means that 68 divided by 34 gave a zero remainder; therefore, 34 is also a factor of 68.Step 5: Within the range known of the number 68, 34 was the last number we could try to verify the factors of 68; therefore, we will now show for 1 and 68 itself:\[ \frac{68}{68} = 1 \]And \[ \frac{68}{ 1} = 68 \]This shows us that both 68 and 1 are also factors of 68. Through these steps, it has become evident that the factors of 68 through the division method are 1, 2, 4, 17, 34, and 68.Factors of 68 through division method: 1, 2, 4, 17, 34, and 68.Factors of 68 by Prime Factorization
The procedure of prime factorization depends on the division of 68 by prime numbers only. The mathematical process involved is the division operation, but some differences exist from the division method.We divide 68 with the smallest possible prime number, producing a composite. We find another prime number that can divide this composite further into another composite number. This process goes on until we reach a final answer of 1. That is our cue to stop this procedure.68 $\div$ 2 = 34
34 $\div$ 2 = 17
17 $\div$ 17 = 1
The prime numbers and the equation for prime factorization are:Prime factors of 68 = 2, 2, 17
The prime factorization of 68 = 2 x 2 x 17
This procedure has also been shown in the figure attached below for a more precise understanding: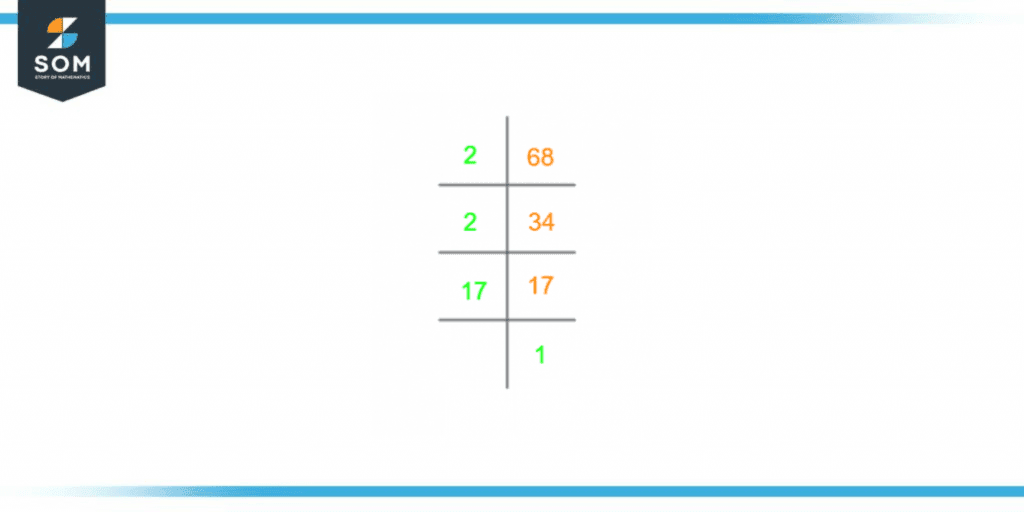
Figure 2 – Prime Factorization of 68
Factor Tree of 68
Factor tree of 68 involves the diagram of a tree to represent the prime factorization of this number. It is drawn in the shape of a tree that branches out into two separate routes after each division step. This division is always done by a prime number only, as we already mentioned that it basically represents prime factorization.Like in prime factorization, the composite number produced is now the new dividend. As long as there is at least one composite number on any of the two branches, the factor tree will continue branching out. But if all prime numbers are reached at a particular stage, that is where the factor tree ends.This definition can be better understood through figure 2, which is attached below: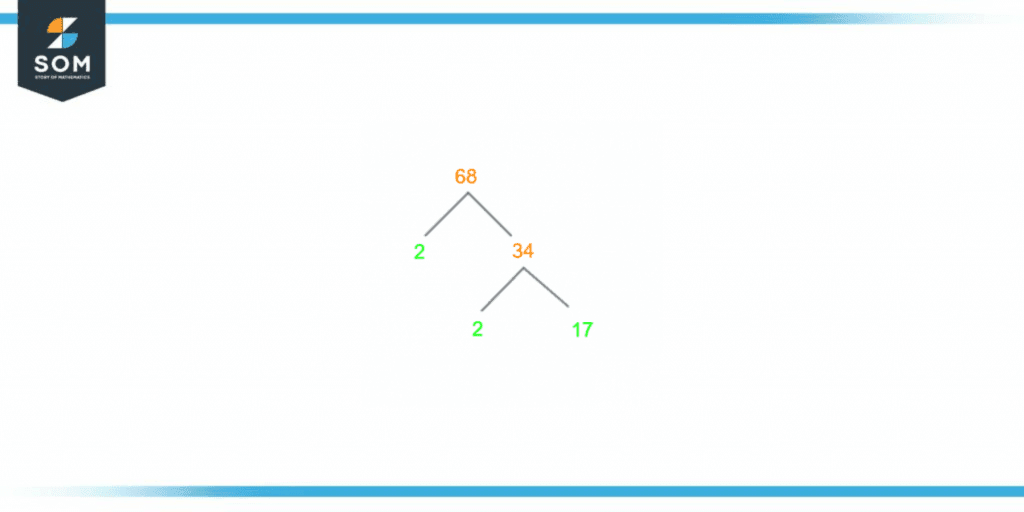
Figure 3 – Factor Tree of 68
Factors of 68 in Pairs
The factor pairs of 68 are any two factors that give 68 when multiplied by each other. Just like all natural numbers can be positive and negative, these factor pairs can also be positive and negative. Before finding out the factor pairs, let us first note down the factors of 68:Factors of 68 = 1, 2, 4, 17, 34, and 68From these factors, we can observe that the pairs which multiply to give 68 are:1 x 68 = 68
2 x 34 = 68
4 x 17 = 68
Now, these pairs are the positive factor pairs of 68:Factor pair of 68 = (1, 68), (2, 34), (4, 17)The negative factor pairs of 68 include an additional negative sign without any other alterations:Negative factor pairs of 68 = (-1, -68), (-2, -34), (-4, -17)Factors of 68 Solved Examples
In this section, we will look at some examples to further improve our concepts of factorization.Example 1
Find out the common factors between 12 and 6.Solution
To find out the common factors of 12 and 6, we will write down the factors of 12 and 6:Factors of 12: 1, 2, 3, 4, 6, and 12Similarly, the factors of 6 are:Factors of 6: 1, 2, 3, and 6To find out the common factors between 12 and 6, we will look at all the numbers that are common between the factors of 12 and 6. These numbers come out to be 1, 2, 3, and 6. So the common factors between 12 and 6 are: Common factors between 12 and 6: 1, 2, 3, and 6Example 2
List down the factors of 68 and calculate their sum. Also, determine its average.Solution
Before jumping to the solution, let’s list down the factors of 68. These factors are given below:Factors of 68 = 1, 2, 4, 17, 34, and 68Now, let’s calculate the sum of these factors. Their sum is given below:Sum of factors of 68 = 1 + 2 + 4 + 17 + 34 + 68
Sum of factors of 68 = 126
Now, let’s move on to calculating the average of these factors. The formula for average is:\[ Average = \frac{\text{Sum of factors of 68}}{\text{Total factors of 68}} \]Inserting the values in the formula:\[ Average = \frac{126}{6} \]Average = 21
Therefore, the average of all the factors of 68 is 21. All images/mathematical drawings are created with GeoGebra.