JUMP TO TOPIC
Factors of 69: Prime Factorization, Methods, Tree, and Examples
All the numbers that perfectly divide the number 69, leave zero in the remainder, and give a whole number in the quotient are called the factors of 69.
Figure 1 – All possible Factors of 69
- 69 is an odd number.
- 69 is a composite number.
- 69 is a semiprime number. Any composite number product of two prime numbers is known as a semiprime number.
- 69 is not a perfect square.
- 69 is a deficient number. It is also known as an insufficient number.
- The cross sum of 69 is 15.
What Are the Factors of 69?
The factors of 69 are 1, 3, 23, and 69.Since 69 is an odd and composite number, it has four positive factors. All the positive factors of 69 in their additive inverse form are called negative factors of 69, which are also 4 in the count for the number 69. It is essential to remember that the number 69 can not have any single negative factor due to its positive nature. The negative factors of 69 must be in pairs.All the above-said numbers are also divisors of 69 because when the number 69 is subjected to dividing by any of the mentioned numbers, it is divided completely and leaves zero or nothing as a remainder.How To Calculate the Factors of 69?
You can calculate the factors of number 69 by the application of the traditional division method. For this intention, start dividing 69 by the smallest natural number that divides 69 entirely without leaving any remainder.Divide 69 by the smallest natural number, which is 1.\[ \dfrac{69} {1} = 69, r = 0\]Since one has divided the dividend by 69 without leaving any remainder ( r = 0) and producing a whole number in the quotient, 1 is a factor of 69.Now divide 69 by the next consecutive natural number, i.e., two, which is also the smallest even prime number.\[ \dfrac{69} {2} = 34.5, r ≠ 0\]Because two has not divided 69 absolutely, and the quotient is a fraction or decimal. Hence, 2 is not a factor of 69. Due to this reason, 69 is called an odd number as it is not divisible by 2.Now try to divide 69 by the next consecutive natural number, which is 3 (smallest odd prime number). Before dividing 69 by 3, we can check either 69 is divisible by three or not by the divisibility test of 3. If the cross sum of any number is divisible by 3, then the number is also divisible by 3. For number 69, the cross sum is 15, which can be divided by 3.\[ \dfrac{69} {3} = 23, r = 0\]The number 69 has been divided completely by its divisor, i.e., 3. Therefore, 3 is also a factor of 69. For attaining more factors, divide 69 by consecutive natural numbers and check that ultimately divide 69 and leave zero remainders. By doing the stated exercise, we will get to know that after 3, 23 is only the number by which 69 can be divided completely.\[ \dfrac{69} {23} = 3, r = 0\]After 23, 69 can not be divided by any other natural number except itself. So, divide 69 by itself are below:\[ \dfrac{69} {69} = 1, r = 0\]It is evident from the division that the number 69 has completely been divided by these numbers and has left no remainder. Therefore, all the numbers 1, 3, 23, and 69 are factors of 69.Salient Facts About Factors of 69
- The natural number 1 is the most minor factor of 69.
- The natural number 69 is the largest factor of the number 69. Keep in mind that the number 69 cannot have any factor larger than itself.
- All the factors of 69 are odd numbers.
- The number 69 has only two prime factors, i.e.,3 and 23.
- For number 69, the sum of factors is 96.
Factors of 69 by Prime Factorization
The representation of the number 69 in the form of multiplication of each of its prime factors is called prime factorization of the number 69. Prime factorization is one of the critical methods that can be utilized to find out the factors of 69.To acquire the goal, divide 69 by the smallest prime number, which divides 69 completely without leaving any remainder. The quotient developed from the division is divided again by the smallest prime number. The methodology continues until 1 is left as the final result, which can no longer be divided by any prime number.Following are the footsteps to find the factors of 69 by the prime factorization method.The first step in the process is to divide 69 by the prime number, which divides 69 perfectly, that is, 3 in this case.\[ \dfrac{69} {3} = 23 \]As the number resulting in the answer is 23, which is also a prime number, it can further be divided by itself only.\[ \dfrac{23} {23} = 1 \]The quotient 1 cannot be divided any further.Therefore, the prime factorization of 69 can be expressed as follows:Prime Factorization of 69 = 3 × 23
69 can also be detonated in the form of its prime factors as:\[ 69 = 3^1 \times 23^1 \]The prime factorization of 69 is also shown in following figure 2.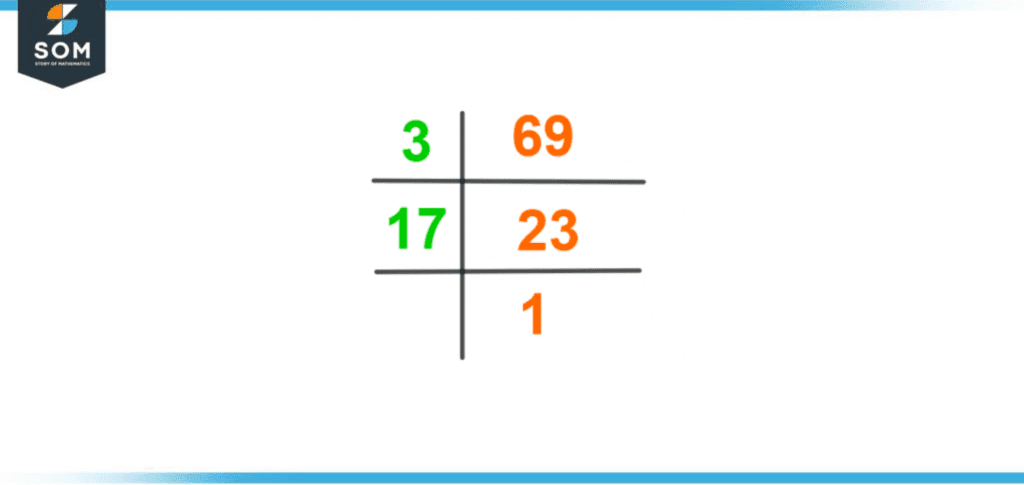
Figure 2 – Prime Factorization of 69
Factor Tree of 69
A factor tree is a distinct way of determining the factors of 69. A factor tree is a pictorial representation where the prime factorization of the number 69 is written in the form of a tree whose branches represent the divisors of the said number.The division of a branch can result in the production of either a prime or composite number. Suppose any of the two sub-divisions resulting from this split generates a composite number. In that case, the division continues to go further until a split generates prime numbers on both arms. This is where the branching or division stops.For the given number, considering the rules of division by the factor tree method, If we write 69 into multiples, it would be;69 = 3 × 23
It is important to describe here that the number 69 has produced prime numbers on both of the branches in its first split. Therefore, it cannot be divided into its further branches. The factor tree of 69 can be represented as following figure 3.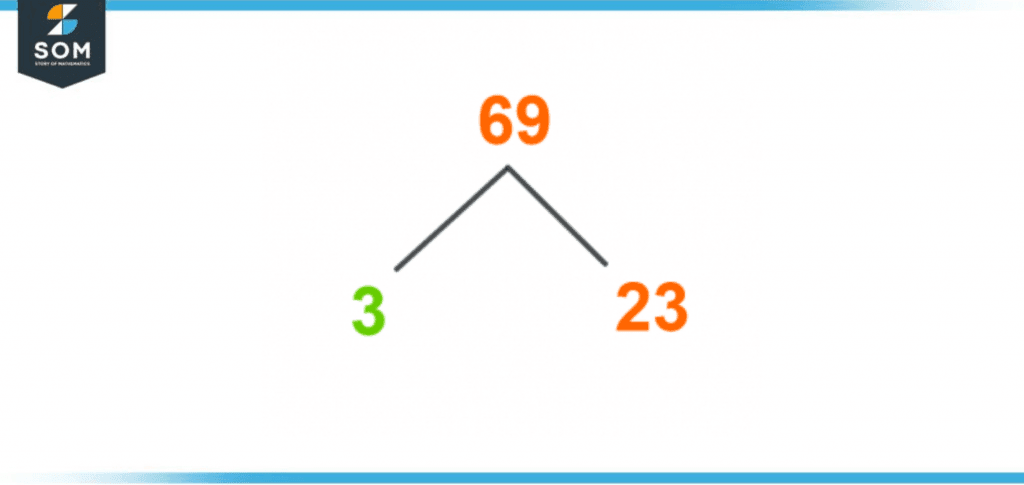
Figure 3 – Factor Tree of 69
Factors of 69 in Pairs
A set of two natural numbers, which are multiplied with each other to generate the number 69, are called factors of 69 in pairs.In other words, it is stated as the product of the factors of the number 69 in the structure of pairs.1 × 69 = 69
3 × 23 = 69
The number 69 has a total of 4 factors which can be written in pairs as below:(1, 69)
(2, 23)
It is kept in the view that when a negative number is multiplied by another negative number, it results in a positive product. Therefore, when all the positive pair factors of 69 in their additive inverse form are multiplied together, it results in a positive 69. Hence, the following are also pair factors of 69.(-1)× (-69) = 69
(-3) × (-23) = 69
Here are the negative pair factors of number 69:(-1, -69)
(-3, -23)
Points To Ponder
- Factors of any number can only be integers and whole numbers.
- Decimals or Fractions can never be factors of any number.
- All the positive pair factors of a number are also pair factors of the same number in their additive inverse (negative) form.
- The number zero can never be a factor of any number.
Factors of 69 Solved Examples
Example 1
The class teacher of Steve gave him a math assignment to find out the average of factors of 69. How will he solve the given problem?Solution
As Steve knows that the average can be found by the sum of all the numbers divided by the count of all numbers. Steve will solve the problem by the following technique:Sum of factors of 69 = 1+3+23+69
Sum of factors of 69 = 96
Count of factors of 69 = 4
Average of factors of 69 = Sum of factors of 69 ÷ Count of factors of 69
Average of factors of 69 = 96 ÷ 4
Average of factors of 69 = 24
Example 2
Why is 69 a semi-prime number?Solution
A semi-prime number is defined as any number which is resulted from the multiplication of two prime numbers.As we know that69 = 3 × 23
In the above equation, both 3 and 23 are prime numbers. Hence, 69 is a semi-prime number.Images/mathematical drawings are created with GeoGebra.