JUMP TO TOPIC
Factors of 75: Prime Factorization, Methods, Tree, and Examples
Factors of 75 refer to the numbers by which 75 can completely be divided or they are those numbers whose product is 75 when two numbers are multiplied together. Hence, the number is referred to as a factor if it divides 75 with a remainder of 0.
Figure 1 – All possible Factors of 75
What Are the Factors of 75?
The factors of 75 are 1, 3, 5, 15, 25, and 75. As 75 is a composite number it has more than 2 factors.The factor pairs are (1,75), (3,25) and (5,15). You can achieve it by pairing the integers so that the result is 75. Whenever 75 is reduced (divided) by these figures, the answer is always 0.How To Calculate Factors of 75?
You can use two methods to determine the factors of 75: division and multiplication method. First, let’s look at how to find the factors through division. Find all the figures that are less than or equal to 75. Then divide 75 by each of the numbers. The factors of 75 are the divisors that cause the remainder to equal 0. To better understand this idea, look at the following example given below. Using the smallest factor of 75 (except 1) which is 3, we divide 75 by 3 which gives us 25. Thus 3 and 25 are the factors of 75. \[ \frac {75}{3} = 25 \]This shows that both divisor and quotient (3 and 25) are factors of 75 as the quotient is a whole number and has no remainder. All the possible divisions of 75 are listed below: \[ \frac{75}{1} = 75 \]\[ \frac{75}{3} = 25 \]\[ \frac{75}{5} = 15 \]\[ \frac{75}{15} = 5 \]\[ \frac{75}{25} = 3 \]Therefore, all the factors are listed below:Factors: 1, 3, 5, 15, 25, 75 Now let’s focus on how to determine the factors through multiplication. In all conceivable ways, represent 75 as the product of two numbers. The factors of 75 are all those integers that are involved in all of these products. For example:1 x 75 = 75
3 x 25= 75
5 x 15= 75
Hence, 1, 3, 5, 15, 25, and 75 are the factors of 75.Factors of 75 by Prime Factorization
One technique to express a particular number as the product of its prime factors is through the method of prime factorization, which involves determining which prime factors can multiply with one another to yield the number as a product. In other words, it is the method of finding or expressing the given number as the product of prime numbers. A prime number only has two factors, 1 and the number itself. Since 75 is a composite number, it ought to contain prime factors. Let’s learn how to determine the prime factors. The very first method is to divide 75 by the smallest prime factor, for example, let’s take 2. 75/2 will yield a fractional number if we divide it, thus we may move on to the following prime number, which is 3. This is shown below:\[ \frac{75}{3} = 25 \]The result of dividing 25 by 3 is a fractional number, which is not a factor. Hence, we proceed to the next prime number that is: \[ \frac{25}{5} = 5 \]\[ \frac{5}{5} = 1 \]After the division process, we received the number 1. Thus, preventing us from moving on. Thereby, the prime factors of 75 mathematically can be represented as:3 x $5^{2}$= 16
The prime numbers in this scenario are 3 and 5. The diagram attached below is the prime factorization of the number 75.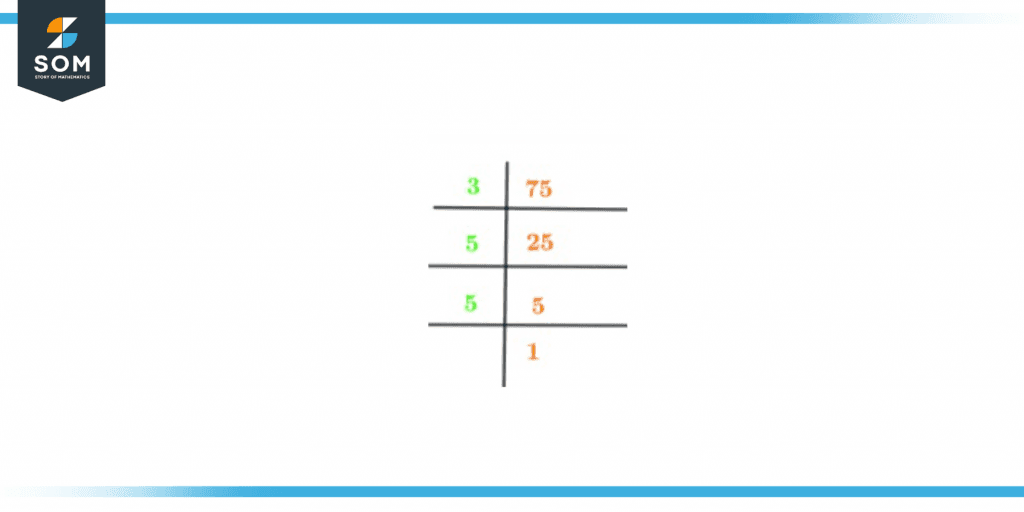
Figure 2 – Prime factorization of 75
Factor Tree of 75
Even the factors of a number can be represented in several different ways. One of the numerous ways to graphically display the prime factors of a particular number is to express factors through a Factor Tree. The number itself is the root of the factor tree, and from there, the branches represent factors until you reach the prime number. Therefore, according to prime factorization 3 and 5 are the prime factors of 75. So, 5 should be the last number to be represented on the factor tree. You can see the Factor tree of 75 attached below: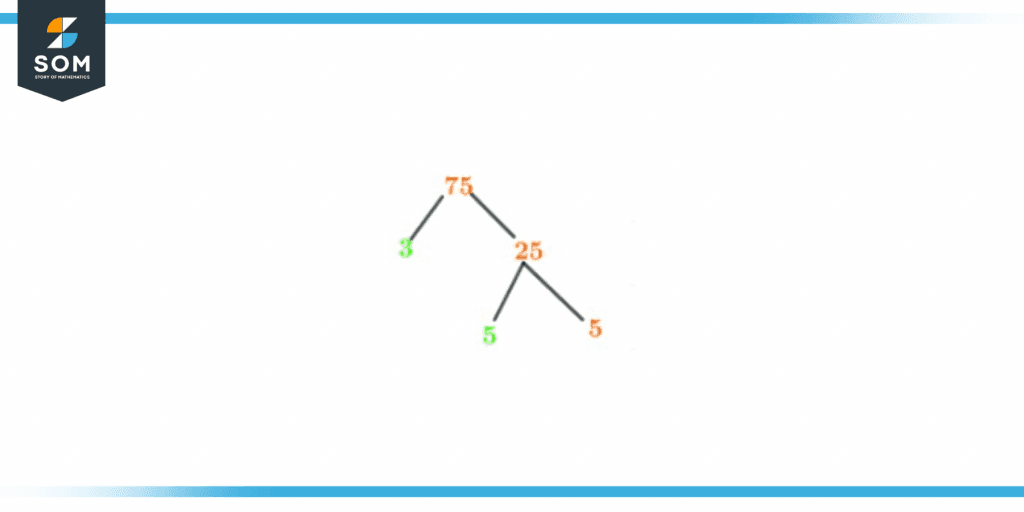
Figure 3 – Factor tree of 75
- The fourth ordered Bell number, 75, tracks the number of weak orderings among a group of four things.
- A pentagonal pyramidal number75 is created by adding the first five pentagonal numbers together. Also, the number 75 is nonagonal and natural.
- 75 is a Keith number. Because there isn’t an integer whose digits when added together equal 75, it is a self-number.
- In the third dimension, there are 75 uniform Polyhedra which include 7 families of prisms and antiprisms.
- 75 is Rhenium’s atomic number and the maximum age for senators from Canada. Furthermore, it is the department number of the city of Paris.
Factors of 75 in Pairs
When multiplied together, a pair of two integers is known as a factor pair which produces the number itself as the result e.g. If 1 multiplied by 75 is 75, then (1, 75) is a pair factor of 75. Similarly, other factor pairs of 75 are as follows:1 x 75 = 75
3 x 25 = 75
5 x 15 = 75
The factor pairs are (1, 75), (3, 25), and (5, 15). Hence, these are the positive factor pairs of 75. To find out the negative factor pair, all you have to do is to reverse the signs. The negative factor pairs are as follows:-1 x -75 = -75
-3 x -25 = -75
-5 x -15 = -75
In conclusion, the only difference between the negative factor pairs and the positive factor pairs is their signs. For that, the entire process of finding factors is the same except that you need to write all the numbers in an expression with a ‘-’ sign to get the negative factor list. The negative factor pairs are (-1, -75), (-3, -25), and (-5, -15).Factors of 75 Solved Examples
To further enhance the concept of factors of 75, let’s take a look at some detailed examples involving factors of 75.Example 1
Find the common factors of 75 and 70.Solution
For finding the common factors between 75 and 70, let’s first list down all the factors of 75. These are given below:Factors: 1, 3, 5, 25, 75Similarly, the factors of 70 are given below:Factors: 1, 2, 5, 7, 10, 14, 35, 70 Thus, the common factors of 75 and 70 are 1 and 5.Example 2
Sam wishes to increase the value of 10 by a natural number so that it becomes a factor of 75. Which number needs to be added?Solution
Theoretically, she will increase 10 by x. As a result, x+10 is a factor of 75. Let’s list all the factors that add up to 75 and are greater than 10: 15, 25, and 75. So, x can either be 5, 15, or 65. This means that Sam can add 5,15 and 65 to 10, for it to become a factor of 75.5+10=15
15+10=25
65+10=75
Therefore, 15, 25, and 75, three of them are factors of 75.Example 3
Find the sum of all the positive factors of 75.Solution
Let’s first list down all the positive factors of 75. These are given below:Positive factors of 75: 1, 3, 5, 15, 25, 75 Calculating their sum:Sum of factors of all factors: 1+ 3+ 5+ 15+ 25+ 75= 124
Hence, the sum of all the positive factors of 75 is 124.