JUMP TO TOPIC
Factors of 74: Prime Factorization, Methods, Tree, and Examples
Factors of 74 are known to leave zero as the remainder and a whole number as the quotient when they act as the divisors for the number 74. This set of natural numbers is classified as the Factors of 74.
Figure 1 – All possible Factors of 74
What Are the Factors of 74?
The factors of 74 are the following: 1, 2, 37, and 74. 74 has four factors, generating zero as the remainder when they act as divisors.These 4 factors of 74 can be paired into 2-factor pairs. These factors can be both positive and negative; the only difference is the sign.How To Calculate the Factors of 74?
You can calculate the factors of 74 through the division method. It is one of the simplest and the most reliable methods for determining the factors of any number. It can be used to determine both the prime factors as well as the composite factors.Before we move on to the division method, let’s first determine the range of the factors of 74. This range indicates the limit in which the numbers have the possibility to be a factor of 74. This range starts from 1 and ends at half of the number. As half of the number 74 is 37, this indicates that all the factors of 74 will lie between 1 and 37. Moreover, as the number 74 is an even number, this also reflects that the number 2 will be one of the factors of 74.Now, let’s move on to the division method. While applying the division method, remember that only those numbers that leave the remainder zero and the quotient as a whole number can be labeled as factors. The divisions of all the factors of 74 are shown below:\[ \frac{74}{1} = 74 \]\[ \frac{74}{2} = 37 \]\[ \frac{74}{37} = 2 \]\[ \frac{74}{74} = 1 \]So, all the possible factors of 74 are mentioned in the list below:Factors of 74: 1, 2, 37, and 74As these factors are natural numbers so their mirrored numbers can also exist. These numbers are the same in value as the positive factors but have negative signs. This originates from the concept of negative factors.Therefore, the negative factors of 74 are given below:Negative Factors of 74: -1, -2, -37, and -74Factors of 74 by Prime Factorization
The prime factorization technique is a specified technique used to determine only the prime factors. These prime factors are all prime numbers. The prime factorization is based on the operation of division. In prime factorization, the whole number quotient produced in every division step takes the place of the dividend in the next step.Another thing to note about prime factorization is that only prime numbers carry out the division process. The division continues until only one value is left at the end.The prime factorization of the number 74 is given below:74 $\div$ 2 = 37
37 $\div$ 37 = 1
This prime factorization can also be written as shown below:Prime Factorization of 74 = 2 x 37
The visual illustration of the process of prime factorization is shown below in figure 2: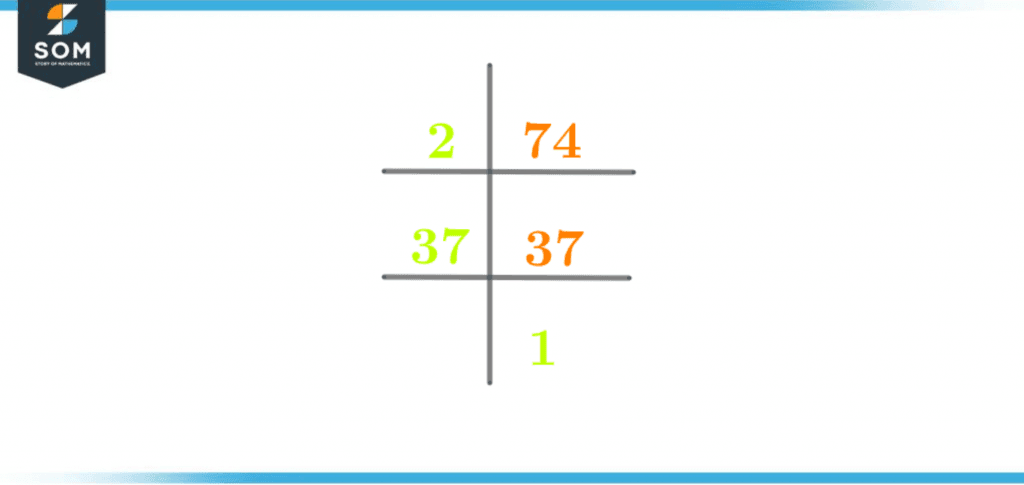
Figure 2 – Prime Factorization of 74
Factor Tree of 74
The factor tree is a visual representation of the prime factors of a number. The factor tree has multiple numbers and branches which originate from these numbers. The factor tree begins with the number itself, and two branches extend out from this number. One of these branches holds a prime number, and the other has the number, which gives birth to additional two branches. The factor tree terminates at branches that both hold prime numbers.The factor tree of the number 47 is shown below: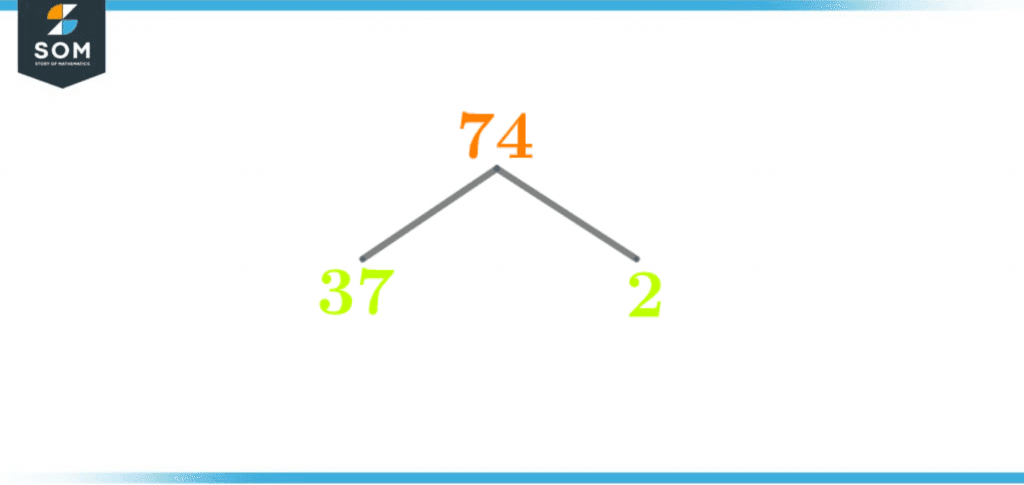
Figure 3 – Factor Tree of 74
Factors of 74 in Pairs
The factors of 74 can also exist in the form of pairs. These pairs are known as factor pairs. A factor pair consists of two numbers that undergo multiplication with each other and result in the original number as the product, in this case, 74.The number 74 has a total of 4 factors, and these four factors can be evenly split into 2-factor pairs. The factor pairs of 74 are given below:1 x 74 = 74
2 x 37 = 74
So the factor pairs are:Factor Pairs of 74 = (1, 74) and (2, 37)As the factors of 74 can also exist as negative numbers, the same goes for factors of 74. These negative factors can be paired in the form of negative factor pairs. The requirement for negative factor pairs is that both the numbers within a factor pair must have negative signs so they can multiply together and generate a positive result.These negative factor pairs are given below:-1 x -74 = 74
-2 x -37 = 74
Negative Factor Pairs of 74 = (-1, -74) and (-2, -37)Factors of 74 Solved Examples
Now that we have covered everything about the factors of 74 and the methods to determine them, let’s move on to some solved examples which incorporate these factors of 74.Example 1
Determine the sum of the factors of 74 and the sum of even factors of 74, find the difference between these two quantities, and determine if it’s a multiple of 2.Solution
To begin with the solution of this example, let’s first list down the factors of 74. These factors are given below:Factors of 74 = 1, 2, 37, and 74Now, let’s calculate the sum of the factors of 74. These factors are summed up below:Sum of factors of 74 = 1 + 2 + 37 + 74
Sum of factors of 74 = 114
The next part is to calculate the sum of even factors of 74. For this purpose, let’s list the factors of 74 that are even numbers. These even factors of 74 are given below:Even Factors of 74 = 2, 74Now, let’s calculate the sum of these even factors. This sum is shown below:Sum of Even Factors of 74 = 2 + 74
Sum of Even Factors of 74 = 76
Now that we have the sum of these quantities, let’s calculate the difference between these quantities. The difference is given below:Difference = Sum of factors of 74 – Sum of even factors of 74
Difference = 114 – 76
Difference = 38
Hence, the difference between the two quantities is 38. The result obtained is an even number, so this indicates that the number 38 is a multiple of 2. This is also evident from the multiplication shown below:2 x 19 = 38
Hence, the number 38 is a multiple of 2.Example 2
Calculate the average of all the factors of 74.Solution
Let’s first list these down to determine the average of all the factors of 74.The factors of 74 = 1, 2, 37, and 74Let’s first look at the average formula to determine the average of these factors. The formula for average is given below:\[ Average = \frac{\text{Sum of factors of 74}}{\text{Total number of factors of 74}} \]\[ Average = \frac{ 1 + 2+ 37+ 74}{4} \]\[ Average = \frac{114}{4} \]Average = 28.5
So the average of all the factors of 74 is 28.5.All images/mathematical drawings are created with GeoGebra.