JUMP TO TOPIC
Factors of 90: Prime Factorization, Methods, Tree, and Examples
Factors of 90 represent a set of integers that divide the number 90 without leaving any remainder behind. Similar to all other numbers, 90 is made up of both positive and negative pairs of factor sets.
Figure 1 – All possible Factors of 90
What Are the Factors of 90?
The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 and 90. All the above-mentioned numbers are the well-recognized factors of the number 90 as these are the set of integers that when divided by the number 90, result in producing zero as the remainder.How To Calculate the Factors of 90?
You can calculate the factors of 90 by using the universally used multiplication or division methods as one of the primary techniques.There are integer factors for 90 that are both positive and negative. The sole difference between the two groups of factors is the way the signs are written; for example, the negative 90 factors are those numerals that, when stated as a mathematical symbol, include a minus sign in addition to the suggested arithmetical value.To begin with, we will multiply several pairs of numbers to get at the required result of 90. Pair-multiplication is the technique used for finding the required factors of 90. Here is the process of how you can find both the positive and negative factors of the number 90. Initially, we are considering the number 1, to be a factor of 90 such that,1 x 90 = 90
The number 1 is also known as the universal factor, as every number when paired and multiplied with 1, results in producing the number itself. Now, we are going to continue and multiply different pairs of numbers to testify whether they are the factors of 90 or not. Is the number 2 a factor of 90?2 x 45 = 90
It is, indeed! Considering that when multiplied by another number, the outcome is 90.3 x 30 = 90
5 x 18 = 90
6 x 15 = 90
9 x 10 = 90
Hence, it has been seen that the numbers 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90 are the factors of 90. We can also say that, the numbers -1, -2, -3, -5, -6, -9, -10, -15, -18, -30, -45 and –90 are the factors of 90.As we have already discussed, the division method is another method for calculating the factors of 90. We will now explain how to compute the factors of 90 using division, which is the other widely used method.Let’s begin by applying the division technique to discover the factors of 90.At first, divide the smallest possible number i.e. 1 with the given number 90. Check for the remainder. Is the remainder zero?\[ \dfrac {90}{1} = 90, r=0 \]Yes, the remainder is zero. Hence, it is proved that the number 1 is a factor of 90.Now, we are going to recommend a few numbers that are less than or equal to 90, divide that number by it, and if the division leaves no or zero remainders, we shall refer to the suggested number as the factor of 90.\[ \dfrac {90}{2} = 45 \]\[ \dfrac {90}{3} = 30 \]\[ \dfrac {90}{5} = 18 \]\[ \dfrac {90}{6} = 15 \]\[ \dfrac {90}{9} = 10 \]Such that, the numbers 45, 30, 18, 15, and 10 are described as the whole-number quotients of the above division processes. As mentioned earlier, each number has both positive and negative factors and the negative factors of any number are the additive inverse of its positive factors. The following is the list of the negative factors of 90.Negative Factors of 90 = -1, -2, -3, -5, -6, -9, -10, -15, -18, -30, -45, -90
Similarly, the following is the list of the positive factors of 90.Positive Factors of 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Factors of 90 by Prime Factorization
Prime factorization is a technique that relies upon the primary method, such as division, to find its route. The goal of prime factorization is to break down an integer into its prime factors until the outcome is 1.Prime factors are integers or numbers that can only be divided evenly by one and by themselves. The prime factor of a given integer can be any number that satisfies the requirements outlined in the definition of prime factors, but never 0 or 1, as these values are not properly classified as prime numbers. The upside-down division is the approach used to find the required prime factors. As per this methodology, the number 90 is initially divided by its smallest divisible prime number, and further divisions are made by dividing the results of the R.H.S. by their respective smallest divisible prime numbers.The prime factorization of 90 is given as,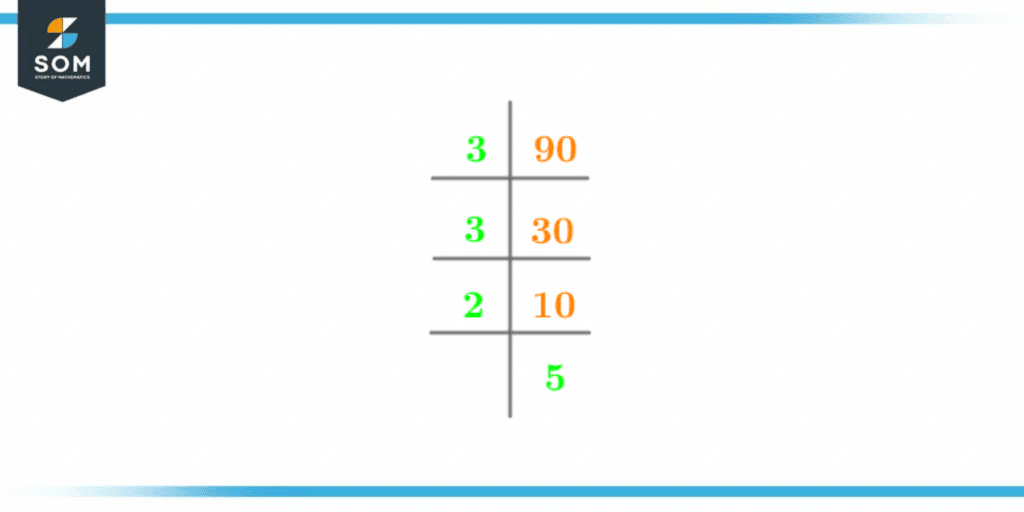
Figure 2 – Prime Factorization of 90
Prime Factors of 90 = 2, 3, 5
Factor Tree of 90
The geometric representation of a number’s prime factors is a factor tree. A factor tree, as its name suggests, contains several branches, each of which specifies a factor with it.The following image shows the factor tree of 90,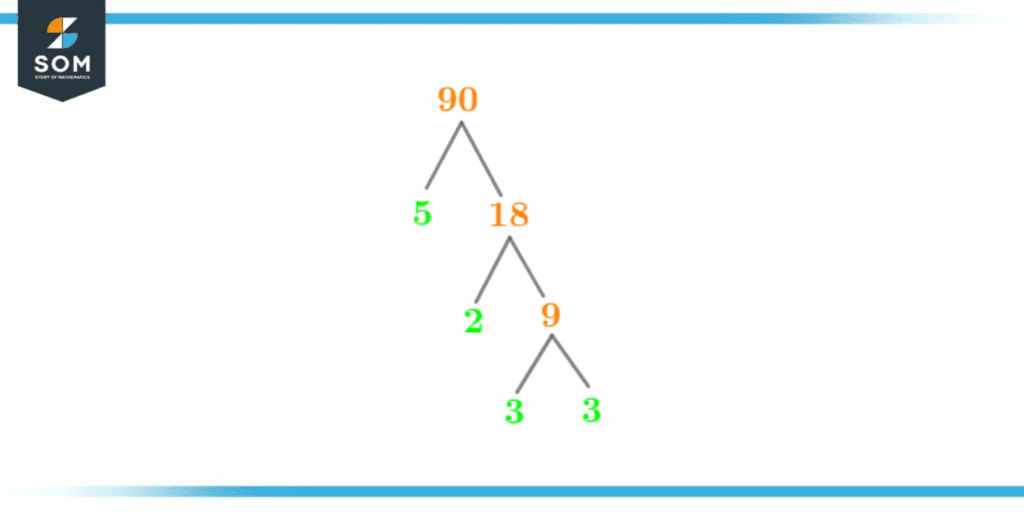
Figure 3 – Factor Tree of 90
Factors of 90 in Pairs
The sets of numbers known as factor pairs are those that, when multiplied together, provide the same outcome as the product of which they are a factor. Both a collection of negative and positive integers may make up the pair of factors. The method for finding the factor pair of 90 is the same as the method for finding the factor pairs of any other integer. Such that, multiplication is the primary technique used to find the factor pairs of 90. Factors of 90 consist of a collection of positive and negative integer pairs, as was previously stated. The pair of factors of the number 90 are represented as:(1, 90), (-1, -90)
(2, 45), (-2, -45)
(3, 30), (-3, -30)
(5, 18), (-5, -18)
(6, 15), (-6, -15)
(9, 10), (-9, -10)
Factors of 90 Solved Examples
Now, let us solve a few examples to test our understanding of the above article.Example 1
Harry designed 90 bags for the newly launched company. All 90 bags were placed in 6 packets. He parceled out x number of bags into 5 packets. Due to the urgency of the job, he neglected to count the total number of bags parceled out and now needs to promptly inform his supervisor of the number. Can you help Harry to calculate the exact number of bags parceled out?Solution
Given that:Total number of bags = 90
Total number of packets = 6
Number of bags parceled out = 5
Total number of bags parceled out = x
We have only one way to determine the exact number of bags parceled out using the factors list of 90.Step 1
We can calculate the total number of bags placed in each parcel such as the factor list of 90 is given as:Factors of 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
\[ \dfrac {90}{6} = 15 \]Step 2
Consequently, the total number of bags distributed across the five packets is given as:15 x 5 = x
15 x 5 = 75
Hence, 75 bags were parceled out in the 5 packets.Example 2
Caroline has been assigned to determine the H.C.F amongst the factors of 90 and 30. Can you help her in finding the exact number from the two-factor lists?Solution
Given that: The list of factors of 90 is given as:Factors of 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Similarly, the factors list for 30 is as follows:Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
Hence, from the above data, we can conclude that the H.C.F amongst the factors of 90 and 30 is 30, respectively. Images/mathematical drawings are created with GeoGebra.