JUMP TO TOPIC
Factors of 900: Prime Factorization, Methods, and Examples
The factors of 900 are the numbers that divide the number 900 exactly without leaving any remainder. For factors, there is a condition that they must divide the original number i.e., 900 exactly, and must have zero remainders.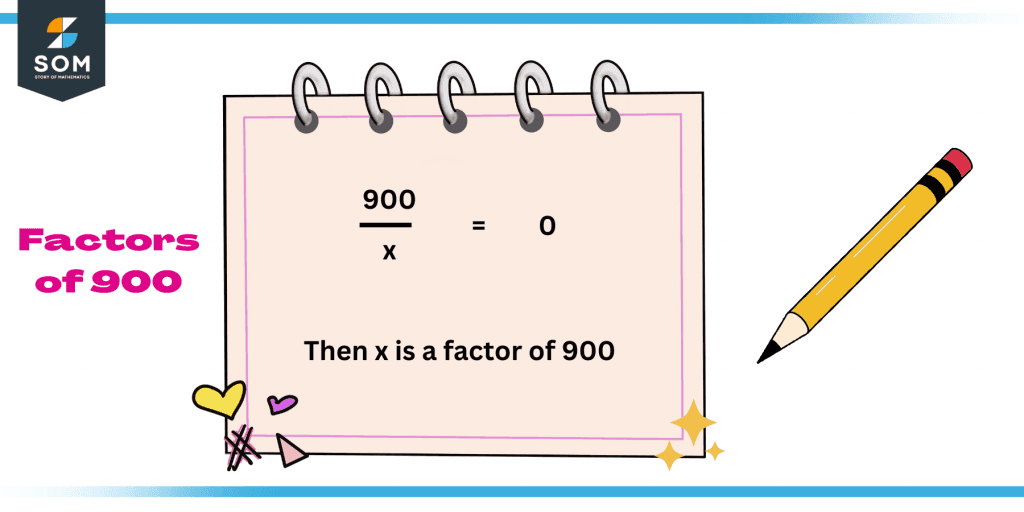
Figure 1 – Method to find the factors of 900
What Are the Factors of 900?
The complete factors of 900 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 30, 36, 45, 50, 60, 75, 90, 100, 150, 180, 225, 300, 450 and 900.All of them when divided by 900, leave zero as the remainder therefore all these numbers are regarded as the factors of 900. Also, note that 1 and the number itself are always the factors of every number. So, 1 and 900 are the factors of 900.How To Calculate the Factors of 900?
You can find the factors of 900 by dividing it by the smallest natural number and if the result in the remainder is 0, then it is a factor of 900. Let’s divide 900 by the smallest natural number i.e., 1.\[\dfrac{900}{1}=900 \]As it has completely divided 900 without any remainder, so 1 is a factor of 900.Now, let’s divide 900 by the smallest even prime number i.e., 2\[\dfrac{900}{2}=450 \]As it has again divided 900 wholly with no remainder, so 2 is also a factor of 900.Now divide 900 with the smallest odd prime number i.e., 3\[\dfrac{900}{3}=300\]As 3 has divided 900 exactly without leaving a remainder, so 3 is also a factor of 900.For getting more factors of 900, it should be divided by natural numbers that exactly divide 900 and bring no remainder as shown below:\[\dfrac{900}{4}=225\]\[\dfrac{900}{5}=180\]\[\dfrac{900}{6}=150\]\[\dfrac{900}{9}=100\]\[\dfrac{900}{10}=90\]\[\dfrac{900}{12}=75\]\[\dfrac{900}{15}=60\]\[\dfrac{900}{18}=50\]\[\dfrac{900}{20}=45\]\[\dfrac{900}{25}=36\]\[\dfrac{900}{30}=30\]\[\dfrac{900}{36}=25\]\[\dfrac{900}{45}=20\]\[\dfrac{900}{50}=18\]\[\dfrac{900}{60}=15\]\[\dfrac{900}{75}=12\]\[\dfrac{900}{90}=10\]\[\dfrac{900}{100}=9\]\[\dfrac{900}{150}=6\]\[\dfrac{900}{180}=5\]\[\dfrac{900}{225}=4\]\[\dfrac{900}{300}=3\]\[\dfrac{900}{450}=2\]Hence, all the above numbers exactly divide 900 without leaving any remainder, so all the above numbers are factors of 900.The negative factors of 900 are exactly similar to its positive factors just with a negative sign.The factor list of 900 is given as:Factors of 900 = 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 30, 36, 45, 50, 60, 75, 90, 100, 150, 180, 225, 300, 450, and 900Factors of 900 by Prime Factorization
To find factors of 900 by prime factorization method, divide 900 by the smallest prime number which divides 900 exactly without any remainder. Then the quotient is again divided by the smallest prime number and the procedure continues until we get the quotient as 1. Following is the method to calculate factors of 900 by prime factorization.First, divide 900 by the smallest prime number which is 2.\[\dfrac{900}{2}=450\]The quotient 450 is a composite number and can further be divided by 2.\[\dfrac{450}{2}=225\]Again 225 is a composite number that can be further divided by 3.\[\dfrac{225}{3}=75\]Now 75 again can be divided further by 3.\[\dfrac{75}{3}=25\]25 further can be divided by 5.\[\dfrac{25}{5}=5\]5 can be further divided by 5.\[\dfrac{5}{5}=1\]The quotient 1 cannot be further divided.Therefore, the prime factorization of 900 can be expressed as:Prime Factorization = 2 × 2 × 3 × 3 × 5 × 5
Prime Factorization of 900 can also be written as:900 = $2^2$ x $3^3$ x $5^2$
The Prime factorization of 900 is also shown in Figure 1 below: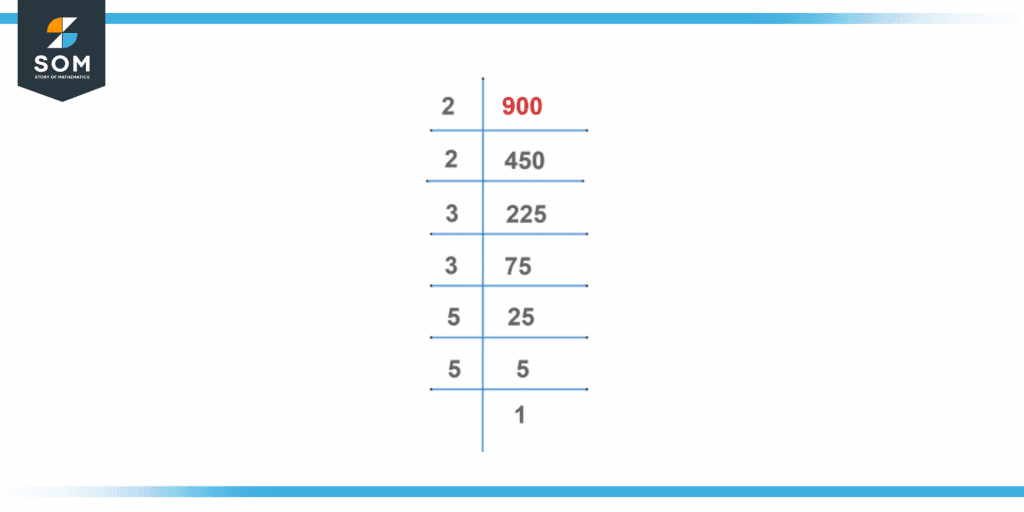
Figure 2 – Prime Factorization of 900
Factor Tree of 900
A factor tree is a way to express the factors of a number, specifically the prime factorization of a number in which each branch in the tree splits into factors. Once the factor at the end of the branch is a prime number, and the other is a composite number, keep on dividing the composite number again unless the only two factors remain, which are itself and 1 so the branch stops.If we write 900 into multiples, it would be 450 × 2.On dividing 450 into its multiples, it would be 225 × 2.On further dividing 225 into its multiple factors, it would be 75 × 3.By splitting 75 further and writing its multiples, it would be 25 × 5.By dividing 25 further into its multiples, it would be 5 × 5.Expressing the number in terms of prime factors would be given as:2 × 2 × 3 × 3 × 5 × 5
The factor tree is shown in figure 2 as: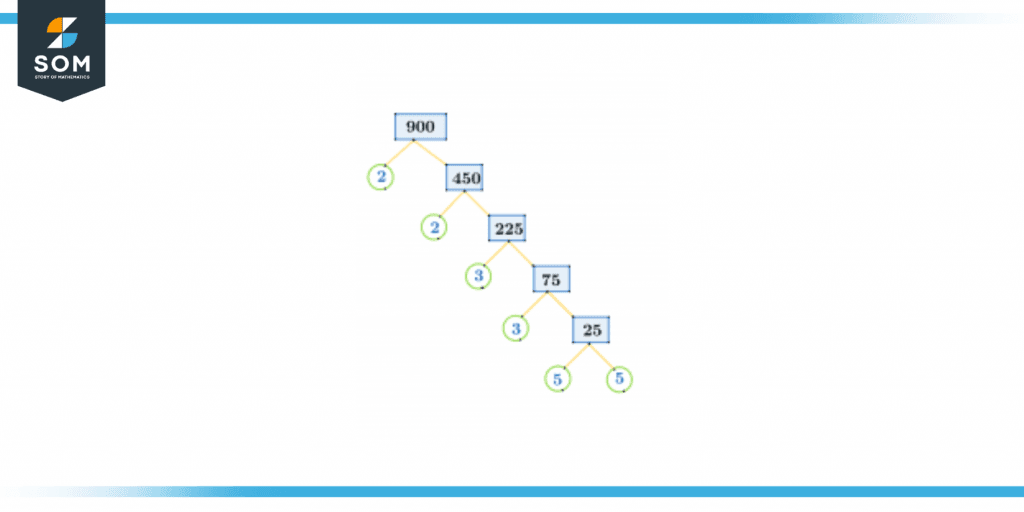
Figure 3 – Factor Tree of 900
Factors of 900 in Pairs
A set of two natural numbers, whose product gives us the number 900, are called factors of 900 in pairs. Pair Factors are a pair of numbers that are multiplied by each other and give the result 900 itself. The factor pairs of 900 can be found as:1 x 900 = 900
2 x 450 = 900
3 x 300 = 900
4 x 225 = 900
5 x 180 = 900
6 x 150 = 900
9 x 100 = 900
10 x 90 = 900
12 x 75 = 900
15 x 60 = 900
18 x 50 = 900
20 x 45 = 900
25 x 36 = 900
30 x 30 = 900
As there are 27 factors of 900, these factors can be written in pairs as follows:(1, 900)
(2, 450)
(3, 300)
(4, 225)
(5, 180)
(6, 150)
(9, 100)
(10, 90)
(12, 75)
(15, 60)
(18, 50)
(20, 45)
(25, 36)
(30, 30)
900 also can have two negative numbers as pair factors. For example:(-12)×(-75)=900
(-6)×(-150)=900
(-3)×(-300)=900
Hence, (-12, -75), (-6, -150) and (-3, -300) are some examples of negative factors of 900.So it can be derived that the product of all factors of 900 in its negative form, gives the result 900. So, they are called negative pair factors of 900.Important Properties
- 900 is a composite number that is also a perfect square.
- 900 is among one of the largest three-digit numbers.
- 900 is also an even number.
- 900 has only 3 prime factors.
- 900 has 27 divisors.
- The square root of 900 is 30.
- The cube root of 900 is 9.
- 450 is the biggest factor and half off of 900 excluding 900 itself.
Factors of 900 Solved Examples
Example 1
Alex has been given 4 sets of pair factors of 900 and has been asked to pick a pair factor with one prime and one composite number. Please help him to pick from the given pair factors options.- (9, 100)
- (15, 60)
- (3, 300)
- (12, 75)
Solution
The factor pair consisting of one prime number and one composite number is (3, 300).Example 2
Which of the following statement is True about factors of 900?- 900 has a total of 27 factors.
- 900 has only three prime factors which are 2,3 and 5.
- (-18, -50) are negative pair factors of 900.
- All of the above.
