JUMP TO TOPIC
Factors of 96: Prime Factorization, Methods, Tree, and Examples
The factors of 96 are integers that uniformly divide the number 96 without leaving any remainder. The number 96 is even composite. The law of division is used.
Figure 1 – All possible Factors of 96
- Division Method.
- Multiplication Method.
What Are the Factors of 96?
The factors of 96 are the following: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. All these divide 96 evenly, leaving the remainder zero. The fact that 96 is an even composite number, it has 24 factors in total. Twelve out of 24 are positive and the remaining twelve are negative factors.- Factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96
- Negative Factors of 96: -1, -2, -3, -4, -6, -8, -12, -16, -24, -32, -48 and -96
- Prime Factors of 96: 2, 3
- Prime Factorization of 96: 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
- Sum of Factors of 96: 252
How To Calculate the Factors of 96?
You can calculate the factors of 96 by the division method and multiplication method. We will learn the division method in this article.Finding factors of 96 using a simple division method:Always remember that the divisor can never be greater than the given number, that is 96. Draw a number line in mind that starts with one and ends on ninety-six. Factors of 96 will be on this number line.In the division method, we simply divide the 96 by a series of numbers from the number line defined above. Always start the division by 1. \[ \dfrac {96}{1} = 96 \]The number 1 divide every number uniformly, leaving the remainder zero. Hence proved that 1 and -1 are factors of 96. Every even number is divisible by 2.\[ \dfrac {96}{2} = 48 \]The remainder is again zero. The numbers 2 and -2 are factors of 96.Divide 96 by 3:\[ \dfrac {96}{3} = 32 \]The remainder is zero. 3 and -3 are also factors of 96.Divide 96 by 4:\[ \dfrac {96}{4} = 24 \]The remainder is zero. 4 and –4 are also factors of 96.Divide 96 by 5:\[ \dfrac {96}{5} = 19.2 \] The remainder is not zero. 5 is not a factor of 96.We will now proceed to divide 96 by a series of numbers:\[ \dfrac {96}{6} = 16 \]\[ \dfrac {96}{8} = 12 \]\[ \dfrac {96}{12} = 8 \]\[ \dfrac {96}{16} = 6 \]\[ \dfrac {96}{24} = 4 \]\[ \dfrac {96}{32} = 3 \]\[ \dfrac {96}{48} = 2 \]The remainder of all the above divisions is zero, and the quotients are an integer.Every number is a factor in itself because every number divides itself evenly. \[ \dfrac {96}{96} = 1 \]96 and -96 are factors of 96.Positive factors of 96 are the following: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. Negative factors of 96 are the following: -1, -2, -3, -4, -6, -8, -12, -16, -24, -32, -48, and -96. Fun Facts:- Factors are never in decimal or p/q form.
- The number 1 is a factor of every integer.
- Every number has positive and negative factors.
- The factor of a number can never be greater than the original number.
- The negative factors of an integer are the additive inverse of its positive factors.
- Factors are never in decimal or p/q form.
- Composite numbers are numbers having more than two factors.
- All even integers have the number 2 as a factor.
Factors of 96 by Prime Factorization
Prime factorization is a technique of denoting a number by its prime factors only. The product of these prime factors is equal to the original number. It is a technique for finding the prime factors of a number. In prime factorization, we split the number into its prime factors.With the help of a simple division method, we can find the prime factorization of 96.Factors of 96 are the following: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.There are two prime numbers in the list of prime factors 2 and 52 and 5 are prime factors of 96.The first step is to dive 100 by the smallest prime factor. The number 1 is not a prime number. \[ \dfrac {96}{2} = 48\]The number 48 is an even number which means it is divisible by 2.\[ \dfrac {48}{2} = 24 \]Again divide by 2:\[ \dfrac {24}{2} = 12 \]\[ \dfrac {12}{2} = 6 \]\[ \dfrac {6}{2} = 3 \]The number 3 is a prime number and not divisible by 2. Now divide it with the next prime factor.\[ \dfrac {3}{3} = 1 \]Obtained 1 as a quotient, we can not proceed further. The figure below shows the division of 96: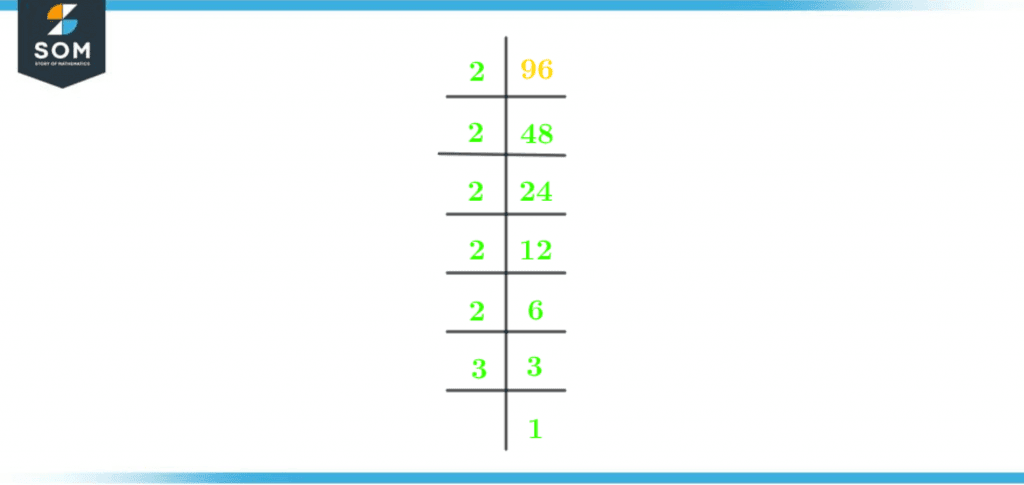
Figure 2 – Prime Factorization of 96
2 x 2 x 2 x 2 x 2 x 3 = 96
Factor Tree of 96
A factor tree is a pictorial way of representing the factors of a number, mainly prime factors. A factor tree starts with the given number and ends at a prime number. The factor tree indicates the numbers that combine to make a more significant number.Write the given number on top, and draw two branches out of it. The left branch will have a divisor, and the right branch will have the quotient. Keep on dividing until both branches possess the prime number.In the case of 96, the number 2 will be the divisor on the radical branch, and 48 will be the quotient. The quotient will be the dividend for the subsequent step. 48 splits into 2 on the right branch and 24 on the left. The number 24 will branch into 2 and 12. When 12 is divided by 2, it produces 6. The number 6 splits into 2 and 3. Both branches are prime, and the factor tree ends. The following is the factor tree of 96: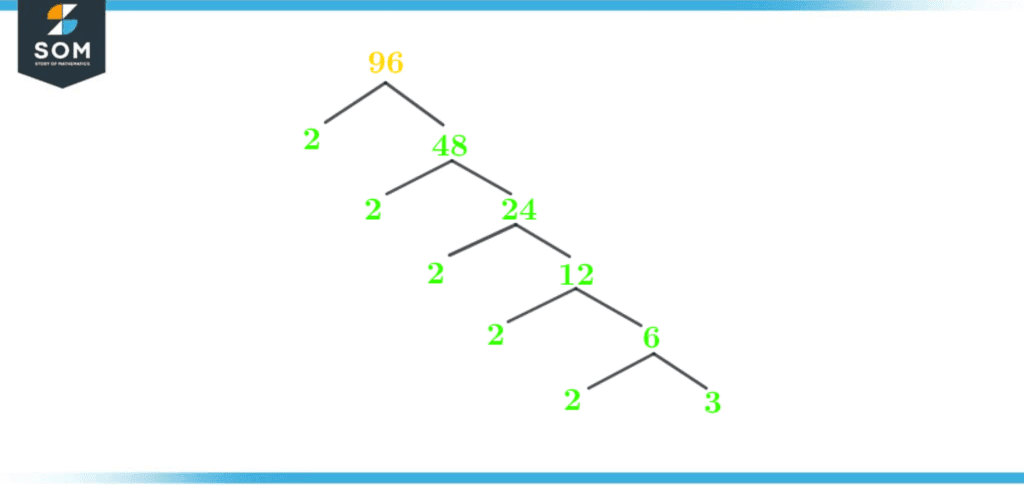
Figure 3 – Factor Tree of 96
Factors of 96 in Pairs
Factor pairs represent the sets of two integers when multiplied give the initial number as a product. Factor pairs can be more than one.Discovering factor pairs by the division method:Factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.\[ \dfrac {96}{1} = 96\]\[ \dfrac {96}{96} = 1\]First-factor pair (1, 96)\[ \dfrac {96}{2} = 48\]\[ \dfrac {96}{48} = 2\]Second-factor pair (2, 48)\[ \dfrac {96}{3} = 32\]\[ \dfrac {96}{32} = 3\]Third-factor pair (3, 32)\[ \dfrac {96}{4} = 24\]\[ \dfrac {96}{24} = 4\]Fourth-factor pair (4, 24)\[ \dfrac {96}{6} = 16\]\[ \dfrac {96}{16} = 6\]Fifth-factor pair (6, 16)\[ \dfrac {96}{8} = 12\]\[ \dfrac {96}{12} = 8\]Sixth-factor pair (8, 12)The number 96 has a total of six positive factor pairs.There are two types of factor pairs:- Positive factor pairs.
- Negative factor pairs.
-1 x -96= 96
-2 x -48= 96
-3 x -32= 96
-4 x -24= 96
-6 x -16= 96
-8 x -12= 96
The law of multiplication says when two negative signs are multiplied their product is always positive.Negative factor pairs: (-1 , -96) (-2 , -48) (-3 , -32) (-4 , -24) (-6 , -16) (-8 , -12)Factors of 96 Solved Examples
Let’s solve a few examples related to the factors of 96 for a better understanding.Example 1
Joey wants to calculate the product(P1) of the sum of prime factors(S1) and the sum of odd factors(S2) of 96. Can you help him?Solution
Yes! We can help Joey.Factors list of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.Prime factors of 96: 2 and 3.Sum of prime factors S1: 2 + 3 = 5Odd factors of 96: 1 and 3Sum of odd factors S2: 1 + 3 = 4Now multiply S1 and S2.Product P1:5 x 4= 20
Example 2
Find the mean of all the factors of 96.Solution
Factors list of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96. Formula to Calculate mean:Sum of all factors/Total number of factors } = Mean
Sum of all factors of 96:1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 + 32 + 48 + 96 = 252
Total number of factors: 12Now put the values in the formula.Mean of 96: \[ \dfrac {252}{12} = 21 \]Images/mathematical drawings are created with GeoGebra.