JUMP TO TOPIC
Factors of 94: Prime Factorization, Methods, Tree, and Examples
Numbers completely dividing 94 will be considered to be the part of factor list of 94. Factors are natural numbers that divide the given number completely and leave the remainder zero.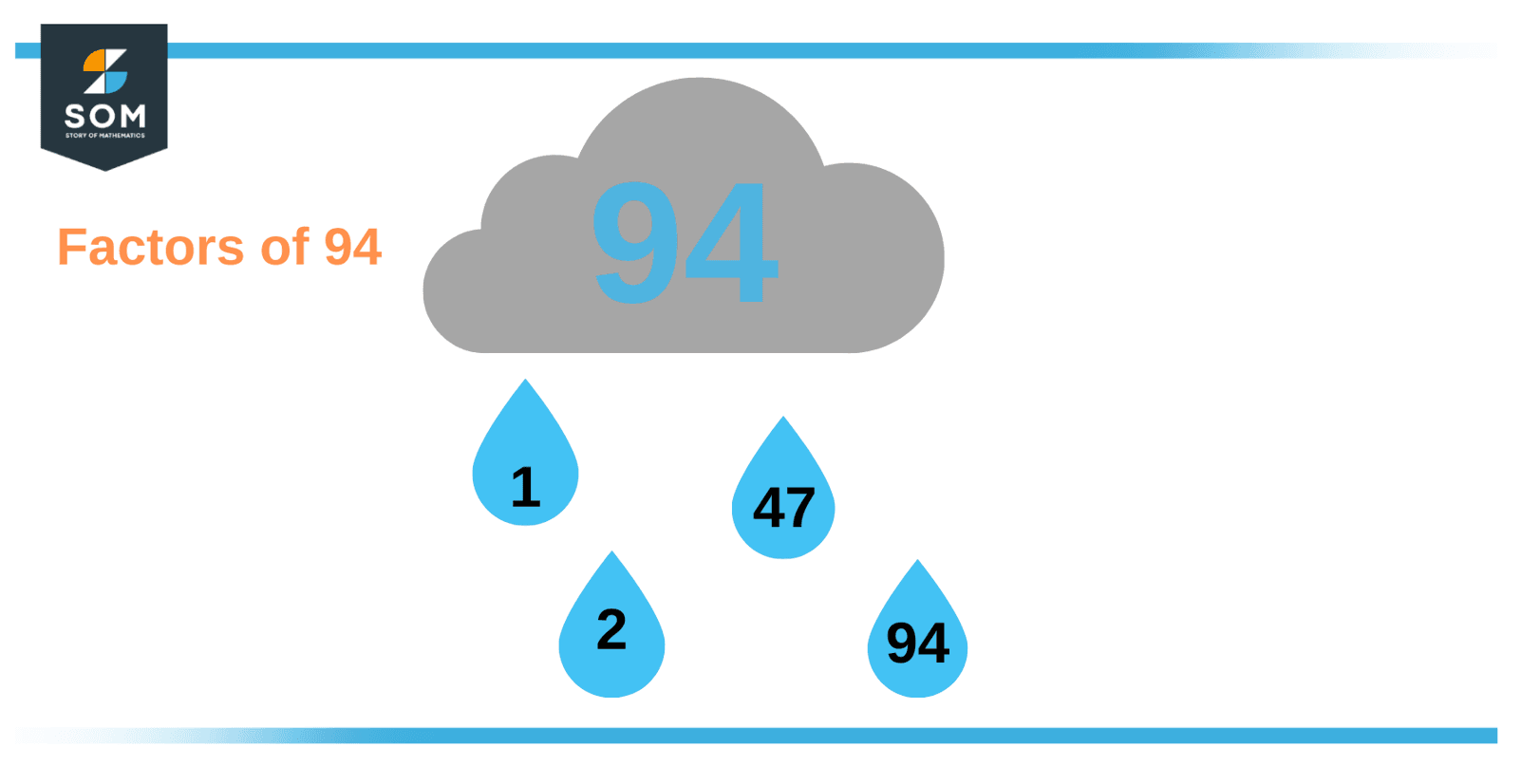
Figure 1 – All possible Factors of 94
The two most common methods to find factors are the Division method and the Multiplication method. We are going to learn how to find factors by the division method as well as by prime factorization. Factors are also known as divisors of the given number.2 x 47 = 94
By the above expression, we understand that if the product of 2 and 47 is equal to 94 this means both numbers which are being multiplied are the factors of 94. In this article, we will learn how to find the factors of 94. After reading this article you will be having a clear understanding of prime factorization, prime numbers, and factor pairs both positive and negative factors. In the end, there are some examples for better understanding and your practice.What Are the Factors of 94?
The factors of 94 are 1, 2, 47, and 94. All these numbers completely divide 94, which means the remainder is zero. The given number 94 is not a prime number so it has more than 2 factors. It has both positive as well as negative factors. 94 has four factors in total. A number that has a total of more than two factors is known as a composite number.How To Calculate the Factors of 94?
You can calculate the factors of 94 by dividing the number 94 by the list of natural numbers from 1 to 94. Numbers that divide 94 evenly are called factors of 94 or divisors of the number. 1 is a factor of every natural number because it divides every number completely, leaving the remainder zero. As a result, 1 will be included in the factor list of every number.\[\frac {94}{1}= 94\] 94 is an even number so it can easily be divided by 2. So we will divide it by 2. \[\frac {94}{2}= 47 \]This means 2 and 47 are also the factors of 94 because both divide 94 completely and the remainder is zero in both cases.Divide 94 by 3:\[\frac {94}{3}= 31.33 \]The remainder is 1, which is a non-zero number so 3 is not a factor of 94.The last factor will be the number itself because every number divides itself fully.\[\frac {94}{94}= 1 \]By the above steps, we conclude that the factors of 94 are 1, 2, 47, and 94. The negative factors of 94 are -1, -2, -47, and -94.The factor list of 94 is given as:Factors of 94 = 1, -1, 2, -2, 47, -47, 94, -94 If the number has an odd number of factors it is a perfect square. 94 has 4 factors 4 is an even number so it is not a perfect square.Factors of 94 by Prime Factorization
Prime factors are factors of a number that are prime numbers. The prime factorization technique is used to express the given number in terms of its prime factors such that its product is equivalent to that number.2 and 47 are prime factors in the list of factors 94. So the prime factorization of 94 is given as:Prime Factorization = 2 x 47
The prime factorization of 94 is shown in figure 1 below: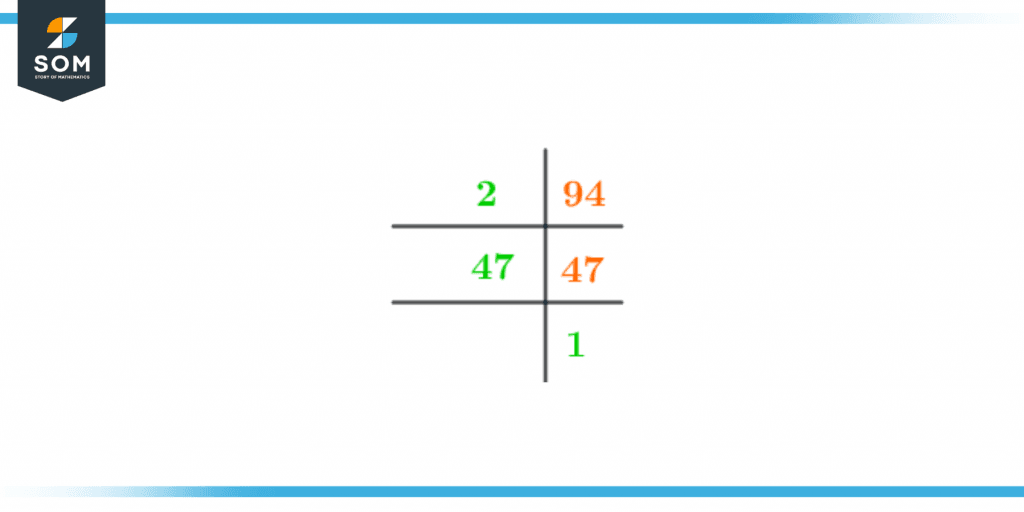
Figure 2 – Prime Factorization of 94
Factor Tree of 94
The pictorial description of a prime factorization of a number is known as a factor tree. The factor tree consists of factorized number at the top further each branch will contain its factors. It is a representation of factors of the given number. The factor tree of 94 is shown below in figure 2: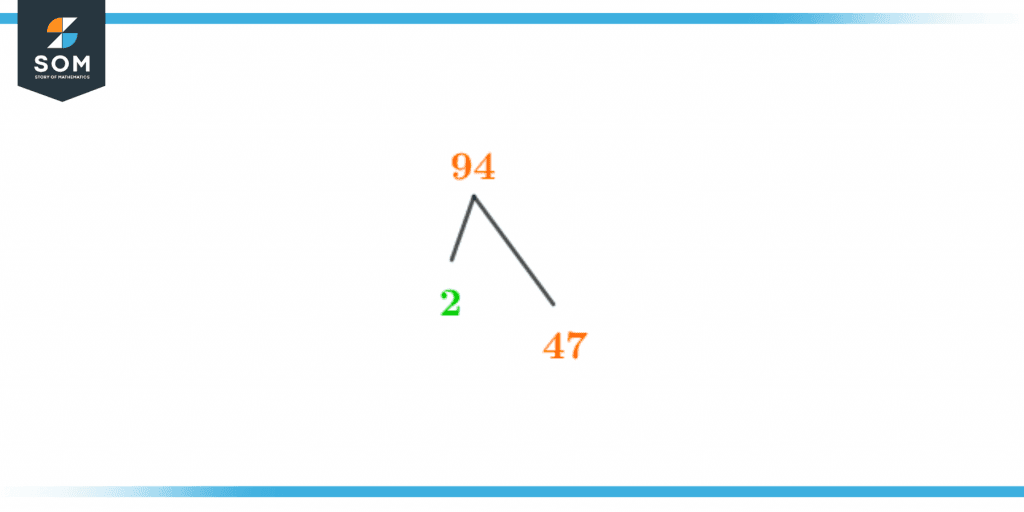
Figure 3 – Factor Tree of 94
Factors of 94 in Pairs
The factor pairs of 94 are the sets of numbers that when multiplied together produce 94 as the result.The factor pairs of 94 are given as:1 x 94= 94
2 x 47= 94
47 x 2= 94
94 x 1= 94
By looking at the above multiplication we will write the factor pairs for 94 as:(1, 94)
(2, 47)
We can also find factor pairs with negative factors of 94 as:-1 x -94= 94
-2 x -47= 94
When a negative number is multiplied by a negative number their product is always positive. Therefore, it is concluded that the negative factors of 94 are nothing but the additive inverse of its positive factors.The negative factor pairs are given as:(-1, -94)
(-2, -47)
Factors of 94 Solved Examples
Let’s solve some examples.Example 1 – Sum of Factors
Find the sum of all factors of 94?Solution 1
Factors of 94 are given as:Factors of 94 : 1, 2, 47, 94The Sum of all factors of 94 is given as:Sum =1 + 2 + 47 + 94
Sum = 144
Example 2 – Common Factors
Find the common factors of 93 and 94.Solution 2
A list of factors of 93 is given below:Factor List of 93 = 1, 3, 31, 93 Factors of 94 are given as:Factors of 94 = 1, 2, 47, 94Common factors mean factors that are part of both lists.Common factors of 94 and 93 are: Common Factors = 1Example 3 – Arranging Factors
Find the factors of 94 and arrange them in ascending order find the sum of the middle 2 factors name it S1 and then find the product of the first and last factor name it P1Arrange factors of 47 in descending order and find the sum of the middle 2 factors name it S2 and then find the product of the first and last factor name it P2- Prove S1 is not equal to S2
- Prove P1 is not equal to P2
Solution 3
Factors of 94 are:Factors =1, 2, 47, 94 Numbers are arranged in ascending order.The sum of the middle 2 factors of 94 S1 is given as:2 + 47 = 49
The product of the first and last factor of 94 P1 is given as:1 x 94= 94
Factors of 47 are:Factors = 47, 1 The factors are arranged in descending order.The sum of the middle 2 factors of 47 S2 is given as:47 + 1 = 48
The product of the first and last factor of 47 P2 is given as:47 x 1= 47
The sum of the middle 2 factors of 94 S1 is 49The sum of the middle 2 factors of 47 S2 is 48.\[ S1 \neq S2 \]From the above results, we conclude that S1 is not equal to S2.The product of the first and last factor of 94 P1 is 94.The product of the first and last factor of 47 P2 is 47.This means P1 $\neq$ P2.From the above results, we conclude that P1 is not equal to P2. Hence, the second statement is correct.Example 4 – Factor Product
Find the product of Even factors of 94.Solution 4
Factors of 94 are 1, 2, 47 and 94Even numbers are those that are divisible by 2 \[\frac {1}{2}= 0.5 \] (1 is not even )\[\frac {2}{2}= 1 \] (2 is even )\[\frac {47}{2}= 23.5 \] (47 is not even)\[ \frac {94}{2}= 47 \] (94 is even )Even Factors of 94 are 2 and 94.Product of Even Factors of 94 is given as: 2 x 94= 188
Images/mathematical drawings are created with GeoGebra.