JUMP TO TOPIC
Factors of 93: Prime Factorization, Methods, Tree, and Examples
Factors of 93 are the numbers that can be divided by 93 without leaving any remainder. For the factors, the condition is that they must be exactly divisible by the given number or must have zero as a remainder when divided. Factors are also known as divisors of the given number.
Figure 1 – All possible factors of 93
In this article, we will be finding the factors of 93. There are several ways to find factors of any number. We are going to learn how to find factors by the division method. After reading this article, you will have a clear understanding of prime factorization, prime numbers, and factor pairs by using positive and negative factors and a factor tree. In the end, there are some examples for better understanding and your practice.What Are the Factors of 93?
The factors of 93 are 1, 3, 31, and 93, as all of them are exactly divisible by 93.The numbers that can completely divide 93 are included in the list of its factors. In other words, the remainder should always be zero. The given number 93 is not a prime number so it has more than 2 factors. It has both positive and negative factors although negative factors are not often considered. 93 has four factors in total. A number that has more than 2 factors is known as a composite number.How To Calculate the Factors of 93?
To calculate the factors of 93, divide it by the smallest natural number which is 1.1 is a factor of all the whole numbers because it divides every number completely which means the remainder is zero.\[ \dfrac{93}{1} = 93,\ r = 0 \]As a result, 1 will be included in the factors list of 93.93 is an odd number, so it cannot be divided by 2. So, we will determine its smallest prime factor which is 3. Now, divide 93 by 3.\[ \dfrac{93}{3} = 31 \]This means 3 and 31 both are factors of 93 because both divide 93 completely and the remainder is zero in both cases.Check for the other natural numbers as well.Dividing 93 by 6 gives:\[ \dfrac{93}{6} =15.5 \]The remainder is 3, which is a non-zero number so 6 is not a factor of 93.Now divide 93 by 9:\[ \dfrac{93}{9}=10.33 \]The remainder is 3, which is also a non-zero number so 9 is also not a factor of 93.The last factor will be the number itself because every number divides itself fully.Following are the numbers that entirely divide the number 93 without leaving any remainder.\[ \dfrac{93}{1} = 93 \]\[ \dfrac{93}{3} = 31 \]\[ \dfrac{93}{31} = 3 \]\[ \dfrac{93}{93} = 1 \]The positive and negative factors of 93 are listed below:Positive factors are 1, 3, 31, and 93.Negative factors are -1, -3, -31, and -93.Properties of Factors of 93
Following are some important properties of factors of 93:- 93 is an odd number therefore, it has no even prime factor.
- The factor of 93 can never be in the form of a decimal or fraction.
- 93 is a semiprime. Semiprime is the natural number that is the product of two prime numbers.
- 93 is also the first natural number in the third triples of successive semiprime numbers. The triplet is 93, 94, and 95.
- The additive inverse of every factor of 93 is also its factor which is called a negative factor.
Factors of 93 by Prime Factorization
Prime numbers are the numbers that have only 2 factors. Those two factors are 1 and the other is the number itself. For example: 2,3,5,7,11….31 etc.(NOTE: 0 and 1 are not prime numbers)Prime Factorization means representing numbers by the product of their prime factors. The list of prime factors contains the factors which are prime numbers. This is an important topic. As mentioned above in the article factors of 93 are 1, 3, 31, & 93. The numbers 3 and 31 are prime numbers because they are not divisible on any number completely except for 1 and itself. So the prime factorization of 93 is 3 x 31. It can be expressed as:93 = 3 x 31
This means when we multiply prime factors of the number the product will be the number itself. In simple words, prime factoring means writing the factors of a number that are prime only.Factor Tree of 93
The factor tree of 93 is shown below in figure 1: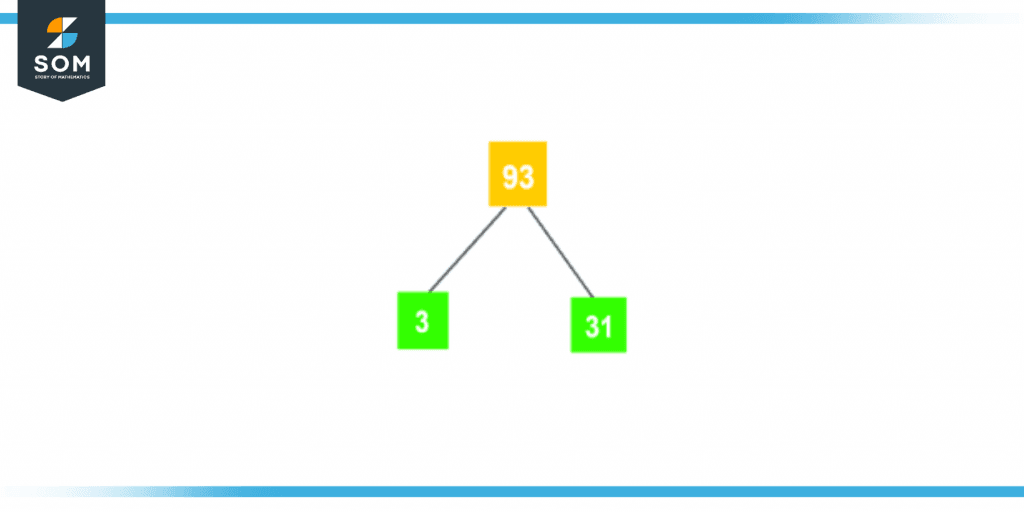
Figure 2 – Factor tree of 93
This diagram is known as a factor tree. The factor tree consists of factors of the number. At the top of the factor tree, each branch will contain its factors. It is a pictorial representation of factors of the given number.By looking at the factor tree, one could easily understand that by multiplying 3 and 31 we will get the original number which is 93.Factors of 93 in Pairs
Pairing the factors of a number means writing them in such pairs that the product must be equal to the number itself.3× 31=93
1× 93=93
The factor pairs for 93 will be (3, 31) and (1, 93).We can also find factor pairs with negative factors of 93-3×- 31=93
-1× -93=93
The negative factor pairs of 93 are (-1, -93), and (-3, -31).When a negative sign is multiplied by a negative sign their product is always positive.Factors of 93 Solved Examples
Following are some solved examples related to factors of 93.Example 1
Find the sum of all factors of 93.Solution
Factors of 93 are 1, 3, 31, and 93.Add up all the factors to find the sum.Sum of all factors of 93 is given as:Sum = 1 + 3 + 31 + 93
Sum = 128
