What Is 1/10 as a Decimal + Solution With Free Steps
 The fraction 1/10 as a decimal is equal to 0.1.
The fraction 1/10 as a decimal is equal to 0.1.
A Decimal Number is just like any other number, but it contains two parts, a Whole Number part, and a Decimal part. The whole number part of the decimal consists of an Integer that is not a decimal value, whilst the decimal part contains only Decimal Values.
The Decimal Values we refer to in this definition are numbers that are smaller than 1, and hence have to be expressed as a fraction of 1. This is where we will introduce the concept of Fractions.
A Fraction is defined as a piece of a bigger object, and that is exactly what fractions represent in mathematics as well. Therefore, a division that leads to a value that lies between two Consecutive Integers would have to be expressed in the form of a fraction.
Now, let’s solve our fraction 1/10 also referred to as One Tenths into its corresponding decimal value.
Solution
To solve a Fraction of a number, we must first understand what it truly means in terms of a division. A fraction can be transformed into a division as the numerator is the Dividend in a division and the denominator is the Divisor.
Dividend = 1
Divisor = 10
Here, the Dividend is the number being divided i.e., broken down into a certain number of pieces. This number is dictated by the value Divisor, which divides the dividend.
So, if we divide 1 by 10, we break 1 down into 10 pieces and take one of those pieces and we have our Quotient, which is the result of a division:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 10
Now, let’s look at the Long Division Solution of our fraction 1/10:
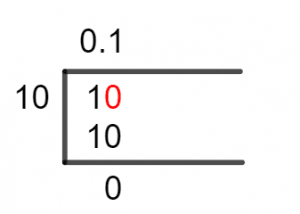
Figure 1
1/10 Long Division Method
The Long Division Method is the most common method for solving divisions that cannot result in a fixed integer value. The process is carried out by finding the Closest Multiple of the divisor to the dividend, as the dividend is not the divisor’s Multiple.
This Multiple must be smaller than the dividend, and the number that produces this multiple of the divisor becomes part of the Quotient. But our work doesn’t end here, as there will be a Remainder after subtracting the multiple from the dividend, which then becomes the new Dividend.
Finally, we need to address one last important piece of information. When solving a division with Long Division Method, a point in time will always be reached. This is when the dividend will become Smaller than the divisor, and when that happens, we bring in the Decimal Point into the Quotient, and along with that, we Multiply the dividend by 10.
Now, looking at our dividend of 1, we multiply it by 10 and place a Decimal in the Quotient where the whole number is 0. Solving for it results in:
10 $\div$ 10 = 1
Where:
10 x 1 = 10
Hence, we have a conclusive solution with no remainder. The Quotient came out to be 0.1.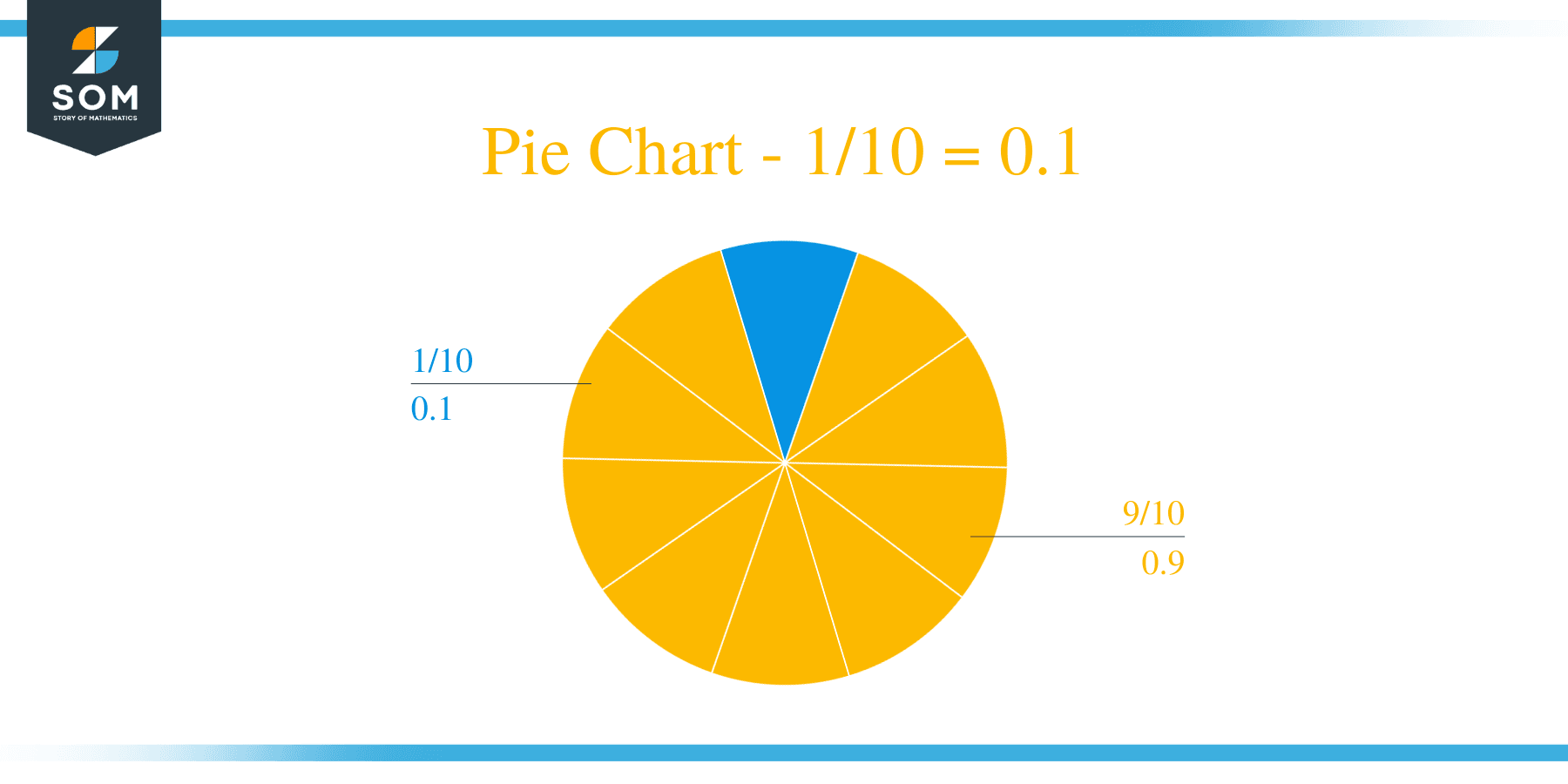
Images/mathematical drawings are created with GeoGebra.
