What Is 1/9 as a Decimal + Solution With Free Steps
 The fraction 1/9 as a decimal is equal to 0.111.
The fraction 1/9 as a decimal is equal to 0.111.
Decimal Numbers are indeed very special as they can express numbers on the number line that lies between Integers. Therefore, they can be of great use in the Real World as things are not all fixed and certain like integers.
Now, as these numbers lie between integer values, their corresponding Fractions are not very easily solved. But there is always a method, and so we have Long Division for solving difficult divisions.
Fractions are widely known as smaller pieces of bigger objects and that is true for numbers as well. So when we have a fraction such as 1/9, it will result in a Decimal Value, and to find that decimal value, we shall solve this through Division.
Solution
Solving a fraction starts by Transforming it into a division, and we know that a division has dividends and divisors. Therefore, the numerator 1 now becomes the Dividend, and the denominator 9 now becomes the Divisor.
Dividend = 1
Divisor = 9
Now, if we divide 1 by 9, it means to Break the number 1 into nine pieces, and take one of those pieces, hence a fraction of 1. As the transformation is completed the Quotient of this division would look like this:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 9
Let’s find the solution to our fraction using the Long Division Method:
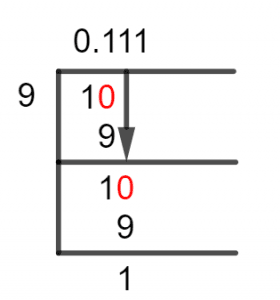
Figure 1
1/9 Long Division Method
This method works by finding the Closest Multiple of the divisor to the dividend and subtracting that multiple from the Dividend. The subtraction will result in a number which will be the Remainder, and this will become the new dividend as the division proceeds.
Now, when solving a division using Long Division, at some point the dividend will become smaller than the divisor, and that is when we introduce the Decimal Point. The decimal point will come into play in the Quotient and the dividend will be multiplied by 10.
Thus, we take a look at our fraction where the dividend is 1 Smaller than the divisor 9, so we have no choice but to introduce the Decimal Point. The whole number will therefore be 0, and the dividend will become 10. Now, let’s solve this:
10 $\div$ 9 $\approx$ 1
Where:
9 x 1 = 9
Hence, a Remainder of 10 – 9 = 1 was produced, as we have a remainder, we shall repeat the process and multiply another ten to the dividend. This makes the Dividend equal to 10 again. So, solving this results in:
10 $\div$ 9 $\approx$ 1
Where:
9 x 1 = 9
A Remainder of 10 – 9 = 1 is produced again, and we can see that the remainder is the same as the last time, and so will be the Quotient. Hence, we can conclude our division here and say that this is a Repeating Decimal Number with the repeating number being 1 and the Quotient being 0.111.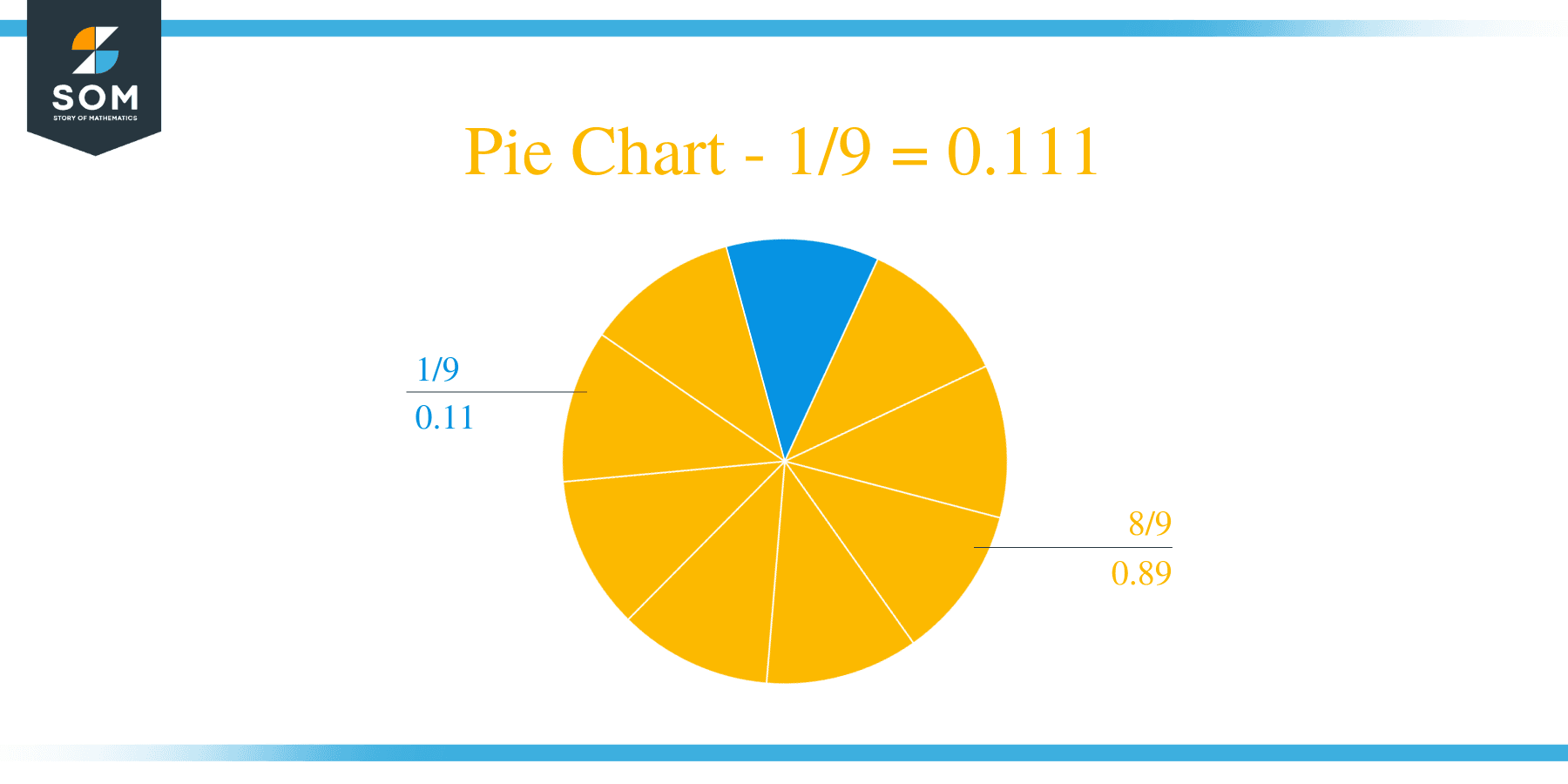
Images/mathematical drawings are created with GeoGebra.
