What Is 1 2/3 as a Decimal + Solution With Free Steps

The fraction 1 2/3 as a decimal is equal to 1.6666666666.
To make Fractions easier to grasp, they are converted into Decimal numbers. Improper fractions, proper fractions, and mixed fractions are the three categories into which fractions can be divided. A fraction is Improper if the numerator is higher than the denominator. A proper fraction refers to a fraction whose numerator is less than its denominator. A fraction containing both a whole number and an Improper fraction is said to be a mixed fraction.
We must apply the division mathematical operator to turn fractions into their decimal equivalents. One of the most challenging mathematical operations is Division. By employing the Long Division approach, we can simplify this.
Solution
The mixed fraction needs to be changed into the p/q form. The fraction’s p is referred to as the Numerator, while its q is referred to as the Denominator. We will add 2 to the product while keeping the denominator constant and multiply the denominator 3 with the whole number 1 to obtain the numerator from the mixed fraction. This leaves us with a fraction of 5/3.
Dividend and Divisor are the two main ideas in the long division method. P is referred to as the dividend, and q is referred to as the divisor in the fraction representation of p/q. The dividend and divider in this case are:
Dividend = 5
Divisor = 3
The solution of the fraction in decimal form is referred to as the Quotient.
Quotient = Dividend $ \div $ Divisor = 5 $ \div $ 3
The long division method for the given fraction is: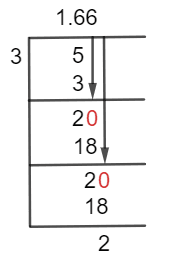
Figure 1
5/3 Long Division Method
The fraction we have is:
5 $ \div $ 3
Here, we can directly divide the two numbers because the dividend is greater than the divisor.
Another key term used in the long division method is “Remainder.” The number remains after the division of numbers that are not wholly divisible.
5 $ \div $ 3 $ \approx $ 1
Where:
3 x 1 = 3
For the remainder, we have 5 – 3 = 2. The remainder is less than the divisor, so to proceed further, we need to add zero to the right side of the remainder. For that, we will add a decimal point to the quotient. By doing so, now we have a new remainder of 20.
Now we will divide 20 by the divisor of 3, and we will get:
20 $ \div $ 3 $ \approx $ 6
Where:
3 x 6 = 18
We now have a remainder of 20 – 18 = 2. Again, we will add zero to the right side of the remainder, and we will get 20.
20 $ \div $ 3 $ \approx $ 6
Where:
3 x 6 = 18
Finally, we have a resulting Quotient of 1.66, with a Remainder of 2.

Images/mathematical drawings are created with GeoGebra.
