What Is 1 1/5 as a Decimal + Solution With Free Steps

The fraction 1 1/5 as a decimal is equal to 1.2.
The quantity of equally sized components combined to create a single, whole thing is expressed as a fraction in mathematics. A Fraction is generally expressed as p/q, where p stands for the numerator and q for the denominator. A numerator produces a whole number if the denominator is divided. Otherwise, a decimal number is produced.
A mixed Fraction is one of the types of Fractions, and it is formed when the whole number and improper fraction are combined together. We use a technique known as Long division. Solving problems of this type is simple using this technique. One of the parts of a decimal number is the whole number, while the other is the decimal component.
There are several methods for converting fractions to decimals in mathematics, but Long Division is the most commonly used.
Solution
We begin by converting the given mixed fraction 1 1/5 into a simple improper fraction by multiplying the denominator 5 by the whole number 1 and then adding the nominator 4, which equals 6/5.
We can now begin to solve a fraction into a division now that we have converted the specified complete fraction into a division. As we know, the numerator equals the Dividend, and the denominator equals the Divisor. As a result, we define our fraction as follows:
Dividend = 6
Divisor = 5
The quantity known as the Quotient is significant in this context because it is produced due to the division of two numbers. Thus, for our Fraction of 6/5, we will write the Quotient as:
Quotient = Dividend $\div$ Divisor = 6 $\div$ 5
The Remainder is the final quantity of importance. This is obtained by subtracting the multiple from the dividend. Furthermore, after each division iteration, the remainder becomes the Dividend.
Let’s finish by looking at the Long Division solution for this problem.
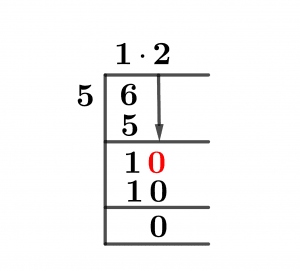
Figure 1
1 1/5 Long Division Method
We have:
6 $\div$ 5
This method is based on the multiple divisors that are closest to the dividend to solve a problem. Not only that, but when our dividend becomes less than the divisor, we multiply it by ten and insert a decimal point into the quotient.
Let us now solve for 6/5:
6 $\div$ 5 $\approx$ 1
Where:
5 x 1 = 5
As a result, a Remainder is generated:
6 – 5 = 1
As a result, because our dividend of 1 is less than the divisor, we multiply it by ten and insert a decimal in the quotient. As a result, our dividend is equal to 10.
So we repeat the process of solving for 10/5, which leads to:
10 $\div$ 5 = 2
Where:
5 x 2= 10
Hence, a Remainder left is:
10 – 10 = 0
Further simplicity is now impossible because the given fraction has been reduced to its simplest form. As a result, the fraction 6/5 equals 1.2, with a remainder of zero.

Images/mathematical drawings are created with GeoGebra.
1 2/3 As A Decimal | Fractions to Decimals List | 7/5 As A Decimal
