What Is 1/25 as a Decimal + Solution With Free Steps

The fraction 1/25 as a decimal is equal to 0.04.
When there is a link between two numbers that include division, a fraction is employed to represent them. There are several methods for solving the fraction, but when one number is not completely divided by another, we usually prefer the long division method.
Here is a thorough explanation of how to calculate the given fraction, 1/25, using the long division method and get its decimal value.
Solution
Before starting to solve the provided problem, it is essential to comprehend the terminology utilized in this approach. The first two ideas we need to understand to divide a fraction are Dividend and Divisor. The dividend is the name of the fraction’s numerator, while the Divisor is the name of the fraction’s denominator. In the given fraction, the dividend is 1 and the divisor is 25, respectively.
Dividend = 1
Divisor = 25
When we solve a problem using mathematical operations, we get the desired results. The result we get after applying the aforementioned method to resolve the fraction is known as the Quotient. It is the fraction’s decimal result.
Quotient = Dividend $ \div $ Divisor = 1 $ \div $ 25
The fraction could get the following result by applying the long division method: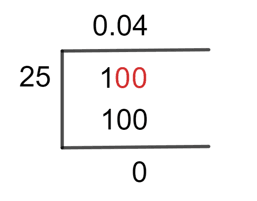
Figure 1
1/25 Long Division Method
Here is a step-by-step explanation of how to solve the given fraction using long division.
The following fraction has to be split using long division:
1 $ \div $ 25
When dividing fractions, there are two situations where the result could be greater than or less than 1. Depending on the dividend and divisor, we have a quotient greater than 1 if the dividend is greater than the divisor, but less than 1 if the dividend is less than the divisor.
Since the numerator of the given fraction, 1/25, is less than the dominator so, we must first add the decimal point before moving on to the solution. We can add zero to the right side of the dividend after adding a decimal point to the quotient.
Before moving on to the solution, it is necessary to define another term, and that term is Remainder. In essence, it is the number that remains after a fraction has been divided.
So by putting a zero on the right side of 1, we get 1, but still less than the divisor. In such a case, we add zero to the quotient, and now we will add another zero to the right side of the divisor. So now we have 100.
100 $ \div $ 25 = 4
Where:
25 x 4 = 100
As a result, we have a remainder of 0, since 100 – 100 = 0. We can now get the resulting Quotient after the remainder has been reduced to zero.
In light of this, the Long Division approach yields a Quotient of 0.04 and a Remainder of 0.
Images/mathematical drawings are created with GeoGebra.
