What Is 9/25 as a Decimal + Solution With Free Steps

The fraction 9/25 as a decimal is equal to 0.36.
A fraction is used to represent numbers when there is a relationship between them that involves division. There are other ways to solve the fraction, but we typically favor the Long Division method when the integers are not entirely divisible by another number.
Thus, a decimal value is obtained by using the long division method on a number that has not been completely divided by another. Long Division can be used to solve the fraction 9/25 as shown below:
Solution
We must comprehend the concepts used in this strategy before we can begin to solve the presented problem. Dividend and Divisor are the first two concepts we must comprehend while dividing a fraction. The dividend is the name of the fraction’s numerator, while the Divisor is the name of the fraction’s denominator. 9 is the dividend and 25 is the divisor in the given fraction.
Dividend =9
Divisor = 25
We obtain the required result when we use mathematical operations to solve a problem. The answer we obtain after resolving the fraction using the aforementioned procedure is known as the Quotient. This phrase essentially refers to the fraction’s best-case result.
Quotient = Dividend $ \div $ Divisor = 9 $ \div $ 25
By using the method called long division, the possible result of the fraction is as under: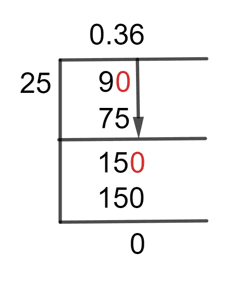
Figure 1
9/25 Long Division Method
Here is a step-by-step explanation of the long division method for solving the given fraction.
The fraction that needs to be divided by using long division is as follows:
9 $ \div $ 25
When dividing fractions, there are two situations in which the result may be greater than or less than 1. Depending on the dividend and divisor. When the dividend is greater than the divisor, we get a quotient that is larger than 1. However, when the dividend is less than the divisor, the resulting value is less than 1.
Since the numerator 9 in the provided fraction 9/25 is less than the dominator 25, we must first add the decimal point to move on to the answer. We can add zero to the right side of the dividend after adding a decimal point to the quotient.
Before moving on to the answer, it is necessary to define another term, and that term is Remainder. In essence, it is the number that remains after an improper fraction has been divided.
The number we now have is 90 after adding a zero to the right side of the dividend.
90 $ \div $ 25 $ \approx $ 3
Where:
25 x 3 = 75
The remainder we have is 15. By adding zero to its right becomes 150.
150 $ \div $ 25 = 6
Where:
25 x 6 = 150
The Remainder we now have is 0 with the resulting Quotient of 0.36 for the given fraction 9/25.
Images/mathematical drawings are created with GeoGebra.
3 7/8 As A Decimal | Fractions to Decimals List | 1/25 As A Decimal
