What Is 1/6 as a Decimal + Solution With Free Steps
 The fraction 1/6 as a decimal is equal to 0.166.
The fraction 1/6 as a decimal is equal to 0.166.
Division refers to either the act of being split apart or the action of breaking something up into pieces. It is a very important concept of mathematics. If compared to multiplication, the division is exactly its inverse.
The division of 1/6 will be performed in the problem to be addressed, using Long Division.
Solution
To perform the given division, the fraction’s components are divided up, based on how they work. When splitting a fraction, the denominator is known as the Divisor and the Dividend is the numerator.
The division that has to be resolved has 1 as a dividend and 6 as a divisor, which has the following fractional form.
Dividend = 1
Divisor = 6
Once the process of division of two numbers is completed, the result we obtained is known as Quotient. But if a division is not completed, the remaining value we get is known as Remainder. Mathematically, we can write the given fraction as:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 6
Using the long division approach, we will simplify this division problem.
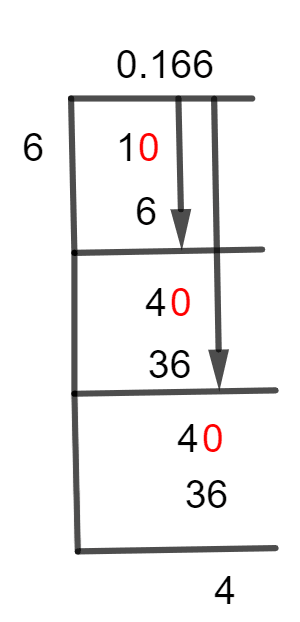
Figure 1
1/6 Long Division Method
A method for dividing large numbers that divides the effort into multiple successive steps is known as Long Division. The dividend is divided by the divisor to get the quotient much like in the conventional division method, and on rare occasions, it results in a remainder.
Following is an explanation of how to use Long Division to solve a given fraction.
We have:
1 $\div$ 6
When performing long division, we determine whether the dividend’s first digit is larger than the divisor. If it is so, we need a Decimal Point to proceed. Thus, we need a decimal point in the example given, since 6 is a greater number than 1.
To get a decimal point, we add a zero to the right of the dividend 1 and have 10. Now we will divide 10 by 6, as shown below.
10 $\div$ 6 $\approx$ 1
Where:
6 x 1 = 6
We know that 10 is not a multiple of 6, so we will get a Remainder of 4 as:
10 – 6 = 4
Now, we again have to put a zero to the remainder’s right but without any decimal point, because Quotient already contains one. After this step, we get 40, which is to be divided by 6.
The resulting value of the remainder, 4 will become 40 after plugging in a zero to its right. Now, the next step can be computed as:
40 $\div$ 6 $\approx$ 36
Where:
6 x 6 = 36
This time remainder is found to be 4.
40 – 36 = 4
As we have the same remainder, calculations of the upper steps are repeated. Thus, Quotient is calculated to be 0.166 and the Remainder is 4. This indicates that 1/6 is a non-terminating fraction.
Images/mathematical drawings are created with GeoGebra.
