What Is 4/5 as a Decimal + Solution With Free Steps
 The fraction 4/5 as a decimal is equal to 0.8.
The fraction 4/5 as a decimal is equal to 0.8.
Division is a primary mathematical operation, and when two numbers are to be divided, they can be expressed in the form of a Fraction, although a fraction is only used when the division doesn’t produce an Integer Value.
Therefore, when we solve the division of a fraction it results in a Decimal Value, which is composed of a Whole Number part and a Decimal Number part. Now, to solve said fraction into a decimal value is also a tricky process, as we rely on a method called Long Division for it.
So let’s go through the Solution of our fraction to decimal conversion for the fraction 4/5.
Solution
We begin by extracting the Dividend and the Divisor from the fraction, which is done by equating the numerator with the dividend, and the denominator with the divisor. This is done for our Fraction as follows:
Dividend = 4
Divisor = 5
Now, we will discuss the most important quantity in a division, and yes, it is the Quotient which is defined as the solution to a division. A Quotient is found by solving the dividend and the divisor as follows:
Quotient = Dividend $\div$ Divisor = 4 $\div$ 5
Hence, we have Transformed the numbers expressed as a fraction into a division, and no we shall look at their solution using the Long Division Method:
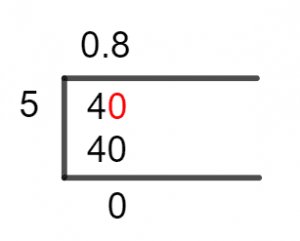
Figure 1
4/5 Long Division Method
The Long Division Method is known for solving the division problems in pieces, and so we will solve 4/5 using Long Division. The process begins by Analyzing the dividend and divisor, whether the dividend is smaller than the divisor or not.
If it is, then the Whole Number part of the decimal number becomes 0 which represents the non-decimal part of the number. We solve the Long Division problems by using the closest multiple of the divisor to that of the dividend. So, once we have that we Subtract that multiple from the dividend to see how far off we are.
This resulting number from the subtraction is thus the Remainder. This will become the new Dividend and the process carries on until we either find the exact Multiple or we have up to Third Decimal Place numbers.
As our dividend is 4 smaller than 5, we begin by Multiplying it by 10 and placing a decimal in the Quotient introducing a Decimal Value. This is done because when solving for a dividend Smaller than the divisor, the only way to solve the problem requires.
So, we will have the dividend as 40, now we solve 40/5:
40 $\div$ 5 = 8
Where:
5 x 8 = 40
Thus, we have a solution where no Remainder was produced, and the divisor was the Factor of the dividend. The Quotient, therefore, comes out to be 0.8 once it is compiled.
Images/mathematical drawings are created with GeoGebra.
