What Is 13/16 as a Decimal + Solution With Free Steps

The fraction 13/16 as a decimal is equal to 0.8125.
A fraction is most commonly expressed as p/q, and Division is what this fraction represents. Now, running division on these two numbers would lead to an equivalent Decimal Value. And to get this decimal value and run the division operation, we use a method called Long Division.
Here, we shall solve the fraction 13/16 using Long Division and find its equivalent decimal value.
Solution
We first set up our fraction into a division representation and express these numbers p and q as the Dividend and Divisor, respectively. Hence, we get the following representation:
Dividend = 13
Divisor = 16
Now, we introduce the Quotient into the division, defined as its solution, given below:
Quotient = Dividend $\div$ Divisor = 13 $\div$ 16
Therefore, the Long Division solution to this problem can be seen given below:
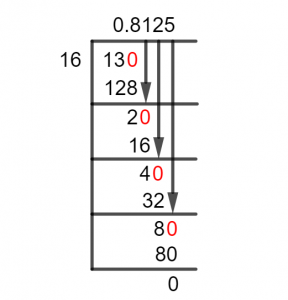
Figure 1
13/16 Long Division Method
Here, we begin to solve our division, and we start with our original Fraction expressed as a division:
13 $\div$ 16
This representation above tells a lot about the final Quotient of this fraction. We can see that the Dividend is smaller than the Divisor and that means the whole number of the decimal value would be Zero and the overall decimal value is smaller than 1.
Now, this is the moment when we go into detail about fractions and their divisions by talking about another quantity of great significance in the Long Division. This is the Remainder, defined as the number that is left as a result of an incomplete division.
It means that the divisor is not a Factor of the dividend and thus we rely on the value smaller but closest to the dividend when solving division.
Thus, when solving for 13/16 we get the resulting remainder of 2. This is done by introducing a zero to the right of the Dividend and getting a decimal point acting on the quotient. Thus, the dividend now becomes 130, and the Quotient gets to a 0.
130 $\div$ 16 $\approx$ 8
Where:
16 x 8 = 128
Hence, the remainder is given by 130 – 128 = 2.
As a Remainder is produced, we must repeat the process either until we have at least three to four values after the decimal point, or a Factor is found. Thus, we have 20 as the new dividend:
20 $\div$ 16 $\approx$ 1
Where:
16 x 1 = 16
Which produces a remainder of 4, thus we carry on and introduce another zero:
40 $\div$ 16 $\approx$ 2
Where:
16 x 2 = 32
Now we have solved this problem up to the third value after the decimal, and our current answer is 0.812, but one may notice that the remainder produced now is 40 – 32 = 8. And that makes 80 after a zero.
Where:
16 x 5 = 80
We have found the factor that concludes this division, and hence the Quotient becomes 0.8125 with no remainder.
Images/mathematical drawings are created with GeoGebra.
