What Is 7/12 as a Decimal + Solution With Free Steps

The fraction 7/12 as a decimal is equal to 0.583.
To express a fraction described as p/q in the form of a decimal number, we use Division. On the other hand, the method used to calculate this division is referred to as Long Division.
Now, we look at the solution for the fraction 7/12 as it is solved to extract a decimal value from it using the Long Division Method.
Solution
We start by referring to this fraction’s components by the names representing their operations. As we are aware, the denominator is called the Divisor, whereas the numerator is called the Dividend. We divide the dividend into the divisor’s number of pieces as a result of Division.
Now we can see:
Dividend = 7
Divisor = 12
Another important quantity in all of this is the Quotient, defined as the solution to a division. Here, we will introduce it into our division.
Quotient = Dividend $\div$ Divisor = 7 $\div$ 12
Thus, after applying Long Division, we get the solution as follows:
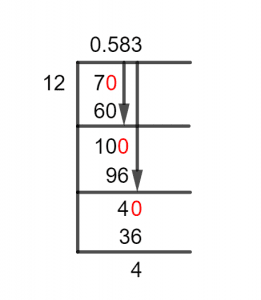
Figure 1
7/12 Long Division Method
Now, we look deeper into the Long Division Solution to this problem, and it begins with:
7 $\div$ 12
In this division, we see that the numerator i.e., the Dividend, is smaller than the denominator i.e., the Divisor. This tells us that the whole number associated with the decimal value will be Zero, as the decimal number will be smaller than one.
Now, to solve this division, we have to introduce a zero to the right of our Dividend, and that brings us to the addition of a decimal point in the quotient. Another vital quantity commonly used in Long Division is the Remainder.
The Remainder is defined as the number that is left once an incomplete division takes place, which means that the divisor is not a factor of the dividend.
And in our result, 10 is a reminder, when we introduce a zero to the right of our dividend which is 7. The process of which gives us 70 as a result:
70 $\div$ 12 $\approx$ 5
Where,
12 x 5 = 60
Therefore, a remainder is produced: 70 – 60 = 10.
Now we repeat the process and bring in another zero to the right of our remainder which now is our dividend. In this case, it is 10 as 10 is less than 12.
Hence, we get:
100 $\div$ 12 $\approx$ 8
Where:
12 x 8 = 96
And we come to find that 12 is not a factor of 100 either. So, we get a remainder of 4 still less than 12, so we repeat the process one last time to get the most accurate result.
40 $\div$ 12 $\approx$ 3
Where:
12 x 3 = 36
Finally, we get a quotient of 0.583 and a remainder of 4, which we could solve further but a three-decimal point is accurate enough that the difference becomes negligible.
Images/mathematical drawings are created with GeoGebra.
