What Is 2 1/2 as a Decimal + Solution With Free Steps
 The fraction 2 1/2 as a decimal is equal to 2.5.
The fraction 2 1/2 as a decimal is equal to 2.5.
The ratio of two whole numbers termed as Numerator and Denominator is called Fraction. Three main types of fractions include proper fractions, improper fractions, and mixed fractions.
A fraction with a greater denominator than a numerator is known as a Proper Fraction, while a fraction with a greater numerator is called an Improper Fraction. However, if a whole number and an improper fraction are combined, we get a Mixed Fraction.
Fractions are usually converted into decimal numbers because they can be easily understood. A number that has a dot separating the fractional part from the whole number part is said to be a Decimal Number and this dot is known as Decimal Point.
In the example, we have to convert a mixed fraction of 2 1/2 into its decimal value by the method of Long Division.
Solution
While converting a mixed fraction into its decimal number, we have to first convert it into an improper fraction. In a given fraction 2 1/2, we multiply denominator 2 with the whole number 2 and add the resultant to numerator 1. The result of these arithmetic operations is the numerator of Improper fraction. While the denominator remains the same. Thus, 2 1/2 is equal to 5/2.
Now to solve this fraction, it is converted into division and we get 5 as a Devisor, the number to be divided, and 2 as a divider, which is termed a Divisor.
Dividend = 5
Divisor = 2
When we divide this fraction, we get our final result known as Quotient.
Quotient = Dividend $\div$ Divisor = 5 $\div$ 2
In some cases, division cannot be performed completely and we are left with some quantity, which is known as Remainder.
Solution of 2 1/2 by Long Division is given here in detail.
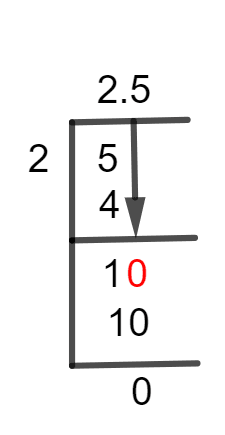
Figure 1
2 1/2 Long Division Method
We want to solve:
5 $\div$ 2
Whenever we have a dividend smaller than the divisor, we need a Decimal Point that we obtain by multiplying our dividend by 10. But if the divisor is smaller, we don’t need any decimal points. Thus, the fraction of 5/2 is divided as:
5 $\div$ 2 $\approx$ 2
Where:
2 x 2 = 4
The remainder is calculated by subtracting 4 from 5.
5 – 4 =1
Since the value of the remainder is less than the divisor, so now we cannot proceed further without a decimal point. Thus, 1 is multiplied by 10 and a decimal point is inserted in the quotient. Now, we have to divide 10 by 2.
10 $\div$ 2 $\approx$ 5
Where:
2 x 5 = 10
This time we get zero remainders.
10 – 10 =0
So, we conclude that fraction 2 1/2 can be solved completely and the value of the quotient is 2 with zero remainders.
Images/mathematical drawings are created with GeoGebra.
