What Is 2 3/5 as a Decimal + Solution With Free Steps

The fraction 2 3/5 as a decimal is equal to 2.6.
Decimal values are more useful in mathematical problems and are simpler to understand as fractions are transformed into decimal values. In most cases, the fraction is expressed in p/q form, where p stands for the Numerator and q for the Denominator.
Fractions fall into one of three categories: improper fraction, proper fraction, or mixed fraction. When the numerator of a fraction exceeds the denominator, the fraction is said to be an Improper fraction.
However, when the fraction’s numerator is smaller than the denominator, the fraction is said to be a proper fraction. A Mixed fraction has both an incorrect fraction and a whole number.
Dividing fractions into decimal numbers is done using the Division operation, one of the trickiest mathematical operations. However, we can simplify it by employing a method known as Long Division. It is a technique for converting fractions to decimal equivalents. Therefore, we are using the long division method to resolve our mixed fraction of 2 3/5.
Solution
We must first change the given mixed fraction into p/q form before moving on to a solution. For that, we’ll add the numerator after multiplying the denominator by the whole number. This will result in the fraction’s p while the denominator remains the same. As a result, we now have a fraction of 13/5.
The terms “Dividend” and “Divisor” are used for the numerator and denominator in the long division method. Therefore, the dividend and the divisors for the fraction are:
Dividend = 13
Divisor = 5
The solution of the fraction is referred to as the Quotient. It is the result of a fraction in decimal form.
Quotient = Dividend $ \div $ Divisor = 13 $ \div $ 5
A fraction can be solved by using the long division method as follows: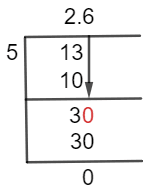
Figure 1
13/5 Long Division Method
The fraction to be solved by the long division method is:
13 $ \div $ 5
If the dividend is greater than the divisor, we can divide the numbers directly. Here we have a case where dividend 13 is greater than the divisor, so we can directly divide both numbers, resulting in a quotient greater than one.
The number left when two numbers are not entirely divisible by one another is referred to as the “Remainder.”
13 $ \div $ 5 $ \approx $ 2
Where:
5 x 2 = 10
After the initial step, the remainder value is 13 – 10 = 3. To move on, we will add zero to the remainder’s right side, changing it to 30. To account for this, we will add a decimal point to the quotient.
30 $ \div $ 5 = 6
Where:
5 x 6 = 30
So we have a Quotient of 2.6 with Remainder = 0 for the given mixed fraction of 2 3/5.

Images/mathematical drawings are created with GeoGebra.
