What Is 3/12 as a Decimal + Solution With Free Steps

The fraction 3/12 as a decimal is equal to 0.25.
Fraction is a term used to represent a small portion or piece of a whole object. For example, 1/4 means one-fourth of an object. If an object is divided into 4 equal parts, then 1/4 is the magnitude or size of one part.
A fraction has two elements, the Denominator and the Numerator. In mathematical calculations, it is difficult to use fractions because these can cause confusion and can also prolong calculations. The solution to this problem is using decimal value instead of fraction. The decimal value of any fraction can be found by division of numerator and denominator. It is a numeric value containing a Decimal Point.
In this section, we will understand the Long Division method for converting a fraction into its decimal value.
Solution
To resolve a fraction, one should have a deep understanding of division. In division, there are two important components, the Dividend, and the Divisor. A dividend is a number, which has to be split into smaller parts. On the other hand, the divisor is the number splitting the dividend.
When a fraction is solved, its component numerator is considered a dividend while the denominator is considered a divisor. So, for 3/12, we can write:
Dividend = 3
Divisor = 12
The decimal number or answer obtained after completing the process of division is called the Quotient.
Quotient = Dividend $\div$ Divisor = 3 $\div$ 12
A residual value at the end of the Division is called the Remainder. A non-zero value of remainder means that the number has not been completely divided.
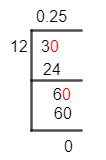
Figure 1
3/12 Long Division Method
Nowadays, although the decimal value of any fraction can be determined using calculators in no time, it is still necessary to learn the conventional division methods to solve fractions. Long Division is an authentic method which has no possibility of errors and provides us with accurate results.
Figure 1 shows the Long Division to solve 3/12.
3 $\div$ 12
We know that the division process requires dividends to be larger than divisors. But we have 3 which is smaller than 12, the divider. Thus, we add a zero to dividend 3 to make it 30 and a decimal point in the quotient.
30 $\div$ 12 \approx 2
12 x 2 = 24
A remaining value greater than zero is generated and is given as:
30 – 24 = 6
This 6 is made 60 by its multiplication with 10 to divide by 12.
60 $\div$ 12 = 5
12 x 5 = 60
As no residual is left behind, so 0.25 is determined to be the decimal value of 3/12. It tells us that when 12 parts, each of size 0.25, are combined, we get a value of 3.

Images/mathematical drawings are created with GeoGebra.
