What Is 5 7/8 as a Decimal + Solution With Free Steps

The fraction 5 7/8 as a decimal is equal to 5.875.
An expression that depicts the mathematical operation of division applied to two numerical is known as a Fraction. The way to represent a fraction is in the form of p/q, where both p and q should be greater than zero.
A resulting number that can be whole or decimal is obtained when both p and q are divided. The term “decimal” refers to any value that falls between two whole numbers.
Decimals are thought to be more comprehensible and feasible to use in arithmetic operations when a comparison is made. As a result, fractions are generally turned to decimal values before being used in calculations or mathematical operations.
This article provides a step-by-step guide for converting a fraction into a decimal using the Long Division method.
Solution
5 7/8 is a type of fraction known as a Mixed Fraction, and it is necessary to be converted into an improper fraction for an accurate solution. The improper fraction equivalent to 5 7/8 is 47/8. Now Long Division will be performed to get our answer.
First, from this fraction, Dividend and Divisor are extracted and are determined as:
Dividend = 47
Divisor = 8
The Quotient or answer of a division is stated as:
Quotient = Dividend $\div$ Divisor = 47 $\div$ 8
If we are left with some value at the end of the division, we call this value the Remainder.
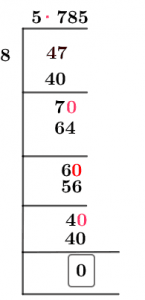
Figure 1
5 7/8 Long Division Method
To show the complete procedure of the Long Division method, an example is illustrated below where a fraction of 5 7/8 is solved.
5 7/8 is equivalent to:
47 $\div$ 8
As we have an improper fraction, 8 will divide 47, as shown in the mathematical details below.
47 $\div$ 8 \approx 5
8 x 5 = 40
After the first step of division, we have 7 as a residual value
47 – 40 = 7
For the next step, 7 is to act as a dividend, but since it is less than 8, the divisor. So, we will continue by putting a Decimal Point in the Quotient and making it 70.
Now 8 will be used to divide 70.
70 $\div$ 8 \approx 8
8 x 8 = 64
Now 70 –64 =6 is acquired by us as the remainder.
Repeating the above process, 6 will be transformed into 60 for the next division step.
60 $\div$ 8 \approx 7
8 x 7 = 56
60 – 56 = 4 is generated value of the remainder this time, which gives us 40.
40 $\div$ 8 = 5
8 x 5 = 40
As 40 is a multiple of 5, zero remainders are produced now.
40 –40 =0.
Therefore, we conclude that fraction 5 7/8 has a decimal value of 5.875 with zero remainders.

Images/mathematical drawings are created with GeoGebra.
