What Is 2/4 as a Decimal + Solution With Free Steps
 The fraction 2/4 as a decimal is equal to 0.5.
The fraction 2/4 as a decimal is equal to 0.5.
A Fraction describes a relationship between two numbers, and this relationship is based on the concept of division. But what makes a fraction special is that it is composed of two numbers that are not multiplicatively related to one another.
Now, if someone were to solve said unsolvable fraction, then it would result in a Decimal Value. And yes, there is a way to solve these inconclusive division problems, and this method is called Long Division.
Let’s take a deeper look at the solution of our fraction 2/4.
Solution
We will begin by extracting the Dividend and the Divisor from this fraction, as we know the numerator is the Dividend and the denominator is the Divisor. We will get the following result:
Dividend = 2
Divisor = 4
Now, we introduce the Quotient which is the result of a division of such sort into our expression:
Quotient = Dividend $\div$ Divisor = 4 $\div$ 25
A Quotient is determined by solving the division between the Dividend and the Divisor.
That is why we can get a lot of information about the Quotient from those two values. As we can see that the Dividend 2 is smaller than 4 so the Quotient will be Smaller than 1. But also, that 2 is a factor of 4 so we would very easily be able to get a conclusive result.
Now, let’s take a look at the Long Division solution of our fraction 2/4:
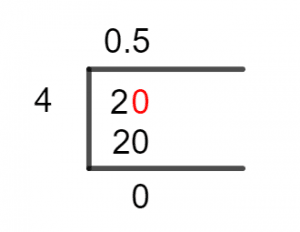
Figure 1
2/4 Long Division Method
As we are now solving a division problem, we express our numerator and denominator as dividend and divisor from now on.
2 $\div$ 4
We have one last significant value to discuss now, and this is the Remainder. The Remainder as we are aware is the remaining value of an incomplete division’s solution. But that’s not even close to how important this value is in the process of Long Division.
The process of Long Division occurs in stages or iterations, we take the dividend and attempt to find the Multiple of the divisor which is the closest value to the dividend. The Difference between the dividend and the divisor is what produces a remainder. If the difference is zero, then the division is complete, and otherwise, the next dividend is then the remainder itself.
And if the dividend is smaller than the divisor then a Decimal Point is added to the quotient, which in turn then adds a zero to the right of the dividend.
So, looking at our fraction’s dividend, we can see that it is indeed smaller than the divisor, so we introduce a Decimal Point and a Zero. This produces a dividend of 20:
20 $\div$ 4 = 5
Where:
4 x 5 = 20
Thus, we have a Complete Division, the dividend is a multiple of the divisor in the first iteration, and there is no Remainder produced. But as a decimal point was introduced before division, the Quotient becomes 0.5.
Images/mathematical drawings are created with GeoGebra.
