What Is 8/11 as a Decimal + Solution With Free Steps
 The fraction 8/11 as a decimal is equal to 0.727.
The fraction 8/11 as a decimal is equal to 0.727.
There are many different types of numbers, and Decimal Numbers are one of them. They are special as they are created by Fractions. A decimal number is composed of two parts, one is the Whole Number part, and the other is the Decimal part.
We know that a Fraction in the literal sense is defined as a smaller part of a bigger object. Similarly, in Mathematics, fractions represent a number broken down into smaller pieces.
So when a number i.e., the Numerator is divided by a denominator, the numerator is broken into a Denominator number of pieces, and one of them is represented by the said fraction. Finally, we talk about the method we use for finding the Solution to a division, this method is called Long Division. So let’s go through the solution of our fraction.
Solution
We begin by taking out the dividend and the divisor from our fraction. As we are aware that the numerator of a fraction is equivalent to the Dividend and the denominator is equivalent to the Divisor, we get the following:
Dividend = 8
Divisor = 11
Now, as we discussed earlier the division within a Fraction can be expressed in a very detailed fashion. For our fraction 8/11, we are dividing the number 8 into 11 pieces and then we grab One of those pieces and that is the value we are chasing. And it can be referred to as the Quotient given as:
Quotient = Dividend $\div$ Divisor = 8 $\div$ 11
Let’s go through the Long Division Solution of this division:
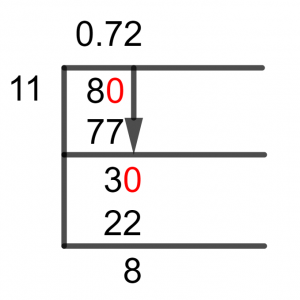
Figure 1
8/11 Long Division Method
When solving a fraction’s division using the Long Division Method, we have to keep two things in mind. One, we multiply the dividend by ten if it is smaller than the divisor and introduce the Decimal in the Quotient. And second, we find the Closest Multiple of the divisor to the dividend and subtract it from the dividend.
This subtraction leads to the generation of a Remainder, and it then becomes the new dividend. Now, as we know our dividend 8 is smaller than 11, let’s introduce the Decimal and make it 80. Solving for it results in:
80 $\div$ 11 $\approx$ 7
Where:
11 x 7 = 77
So a Remainder of 80 – 77 = 3 is produced, and solving further would give us the new dividend as 30, hence we have:
30 $\div$ 11 $\approx$ 2
Where:
11 x 2 = 22
In this iteration, a Remainder equal to 30 – 22 = 8 is produced, and we can see that this has produced our initial dividend again for us. We can solve once more for accuracy:
80 $\div$ 11 $\approx$ 7
Where:
11 x 7 = 77
Therefore, we have a Repeating set of remainders, 3 and 8, and thus we have a repeating decimal number as the Quotient which is 0.727.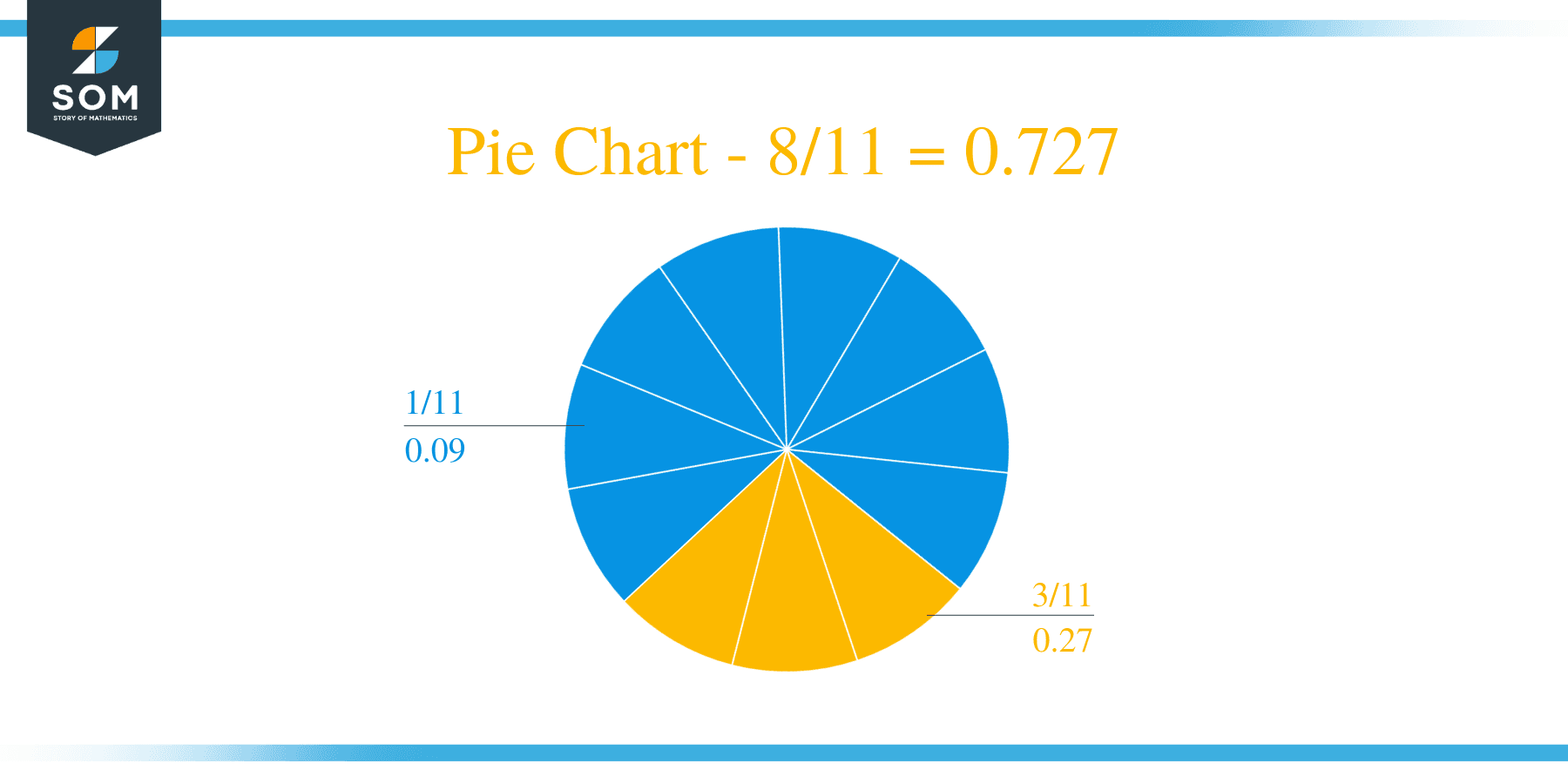
Images/mathematical drawings are created with GeoGebra.
