What Is 9/10 as a Decimal + Solution With Free Steps
 The fraction 9/10 as a decimal is equal to 0.9.
The fraction 9/10 as a decimal is equal to 0.9.
When the numbers have a relationship of division, the Fraction is used to represent it. Multiple methods can be used to solve the fraction but in the case of having numbers that are not completely divisible by another number, we mostly prefer a method called Long Division.
So by using the long division method, the number not fully divided by others ends up in a Decimal value. The fraction 9/10 can be solved by using the Long Division method.
Solution
Before starting the solution to the given problem, we need to understand the terms involved in this method. In the division of fractions, the two terms first we need to understand our Dividend and Divisor. The numerator of the fraction is named the Dividend while the denominator of the fraction is known as Divisor. In the given fraction, 9 is the Dividend and 10 is the Divisor.
Dividend = 9
Divisor = 10
When we solve a problem using mathematical operations, we end up having some desired results. After solving the fraction through above mention method, the result we get is known as the Quotient. This term is the final possible solution to the fraction.
Quotient = Dividend $\div$ Divisor = 9 $\div$ 10
By using the method called Long Division, the possible result of the fraction is as under: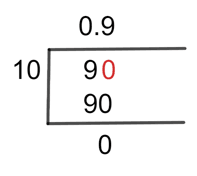
Figure 1
9/10 Long Division Method
Here is the Long Division method discussed step by step to solve the given fraction.
The fraction to be solved by the long division method is given as:
9 $\div$ 10
While solving the fractions we can have two cases in which the result of the division can be greater than 1 or less than 1. It depends on the terms Dividend and Divisor. If the Dividend is greater than Divisor, then we have a Quotient greater than 1, but in the case of having a Dividend less than the Divisor, the resulting value will be less than 1.
In the given fraction 9/10, it can be seen that we have numerator 9 which is less than the dominator 10, so first, we have to add the Decimal Point to proceed with the solution. After adding a decimal point to the Quotient, we can add Zero to the right side of the Dividend.
Another term is required to be introduced before proceeding with the solution and the term is Remainder. It is the number that is left after the division of improper fractions.
By adding Zero to the Right side of the Dividend, the number we now have is 90.
90 $\div$ 10 = 9
Where:
10 x 9 = 90
By doing this, we have a Remainder of 0 because 90 – 90 = 0.
Hence, by using the Long Division method, the resulting Quotient is equal to 0.9 with the Remainder of 0.
Images/mathematical drawings are created with GeoGebra.
