What Is 11/16 as a Decimal + Solution With Free Steps?
 The fraction 11/16 as a decimal is equal to 0.6875.
The fraction 11/16 as a decimal is equal to 0.6875.
Division could appear to be the most complex of all mathematical operations, but it is not that difficult because there is a way to handle this difficult issue. Long Division is the process of answering the question in fractional form.
Here is a comprehensive explanation of how to use the long division method to solve the given fraction, 11/16, and generate the decimal equivalent.
Solution
When we talk about the fraction it consists of two parts. The part above the fraction is known as the Dividend, and similarly, the lower part of the fraction is known as the Divisor.
Dividend = 11
Divisor = 16
When we solve the fraction, we produce a new term known as Quotient, which is the result of the fraction.
Quotient = Dividend $\div$ Divisor = 11 $\div$ 16
Now, by using the Long Division we can solve the problem as: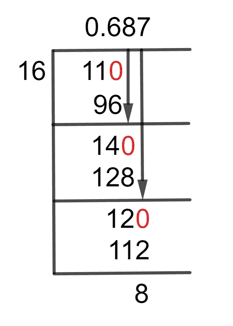
Figure 1
11/16 Long Division Method
Here are the steps of the Long Division method through which we can solve the desired division.
We had:
11 $\div$ 16
Since we have to divide the two numbers and in this case, we have a numerator value less than the denominator value, i.e. 11 is less than 16. So we have to add the decimal point first, after doing this we can multiply our Dividend by 10 and it will become 110.
After dividing the terms, the remaining part is referred to as the Remainder.
110 $\div$ 16 $\approx$ 6
Where:
16 x 6 = 96
This indicates that a Remainder was also generated from this division, and it is equal to 110 – 96 = 14. So after the first step, we have a remainder of 14.
Since we have a remainder less than the divisor, so will multiply 10 with the remainder but this time no need to add the decimal point again because it already has been added with the Quotient.
From the previous step, the Remainder we have is 14. So by multiplying it by 10 we get 140. So in the next step, we will divide the remainder with the divisor to further proceed with the method, and again no need to add the decimal point again because it is already in the quotient.
140 $\div$ 16 $\approx$ 8
Where:
16 x 8 = 128
The remainder we have after solving this is 12, so by multiplying it by 10 we now have 120. So for the third decimal point, the solution is as follows:
120 $\div$ 16 $\approx$ 7
Where:
16 x 7 = 112
As a result, we have a resultant Quotient of 0.687 and a Remainder of 8. This suggests that if we keep solving, we might be able to get a more accurate and precise answer.
Images/mathematical drawings are created with GeoGebra.
5/12 As A Decimal | Fractions to Decimals List | 9/10 As A Decimal
