What Is 5/12 as a Decimal + Solution With Free Steps
 The fraction 5/12 as a decimal is equal to 0.416.
The fraction 5/12 as a decimal is equal to 0.416.
A mathematical expression that tells the number of equal parts into which an object can be divided is known as a Fraction. There are two elements of a fraction that are separated by a slash or line. These are Numerator and Denominator, present above and below the slash, respectively.
Usually, fractions are solved by dividing the numerator with the denominator to get its equivalent decimal. In the fraction of 5/12, 12 is a denominator while 5 is a numerator.
Here, we will demonstrate the method of Long Division to simplify a fraction.
Solution
To get the solution of a fraction, we begin by converting it into division. By doing so, the numerator of the fraction that is present above the slash becomes a Dividend, and the denominator present below the slash becomes a Divisor. Therefore, in this example, we get a dividend of 5 and a divisor of 12.
Dividend = 5
Divisor =12
Fraction 5/12 means to divide the number 5 into 12 equal parts and in the results, we get a numerical value of 1 part, also known as the Quotient. In some cases, fractions are not solved completely and we have a left-over value known as Remainder.
Quotient = Dividend $\div$ Divisor = 5 $\div$ 12
Now, let us solve a fraction of 5/12 as an example.
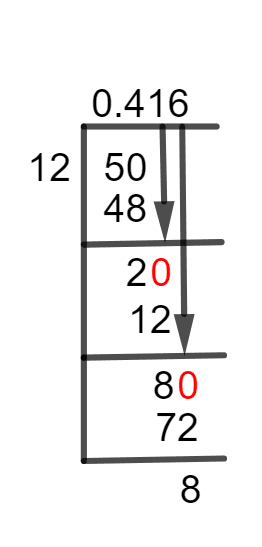
Figure 1
5/12 Long Division Method
An explanation of the Long Division method to solve a fraction is given below.
The fraction given to solve is:
5 $\div$ 12
We know that 5/12 is a Proper Fraction because 5 is less than 12. In a proper fraction, we must introduce a Decimal Point, which can be done by adding a zero to the right of the dividend. The dividend in our case is 5. By inserting a zero to its right we get 50. This 50 can now be divided by 12 as:
50 $\div$ 12 $\approx$ 4
Where:
12 x 4 = 48
As remainder 50 – 48 = 2 is a non-zero value, so we again put a zero to the right of the remainder i.e., 2, and make it 20. But here we don’t need another decimal point.
20 $\div$ 12 $\approx$ 1
Where:
12 x 1 = 12
Now, the remaining value is 8 as shown below:
20 – 12 = 8
When we plug in a zero to right of 8, it becomes 80, which can be divided by 12 as:
80 $\div$ 12 $\approx$ 6
Where:
12 x 2 = 72
This time, the Remainder 80 – 72 = 8 is the same as that obtained in the last step. This shows that it is a non-terminating and recurring fraction with a repeating decimal number. Thus, the Quotient of the given fraction is 0.416 and the remaining value is 8.
Images/mathematical drawings are created with GeoGebra.
