What Is 7/9 as a Decimal + Solution With Free Steps
 The fraction 7/9 as a decimal is equal to 0.777.
The fraction 7/9 as a decimal is equal to 0.777.
In mathematics, we employ a Division operation to split a number into equal parts. Division frequently appears to be more challenging than other mathematical processes. However, there is a way to simplify this extremely complex process. Long Division is the method employed here to solve the given fraction.
The mathematical operation of dividing large numbers into smaller and more manageable units or groups is known as Long Division. It helps to simplify complex and difficult problems.
Here, we will simplify the fraction 7/9 by the Long Division method and will find its equivalent decimal number.
Solution
Separating a division problem into its constituent parts according to each one’s functionality is the first and most significant step in solving the problem. The Dividend is the number that is divided, and Divisor is the number that is used to divide the dividend. The following problem has a dividend equal to 7 but a divisor equal to 9.
In the presented problem, we have:
Dividend = 7
Divisor = 9
Quotient and Remainder are the other two important terms associated with division. A fraction can be divided completely to produce a quotient, which is the result of the division. But a partial division produces a remainder, which expresses the value that remains after an incomplete division.
Quotient = Dividend $\div$ Divisor = 7 $\div$ 9
Here, the decimal value of 7/9 is determined by using the Long Division method.
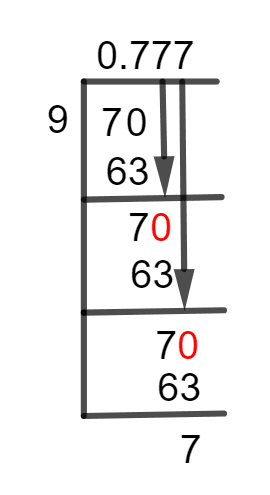
Figure 1
7/9 Long Division Method
The detailed steps to simplify the given fraction are shown below.
We possess:
7 $\div$ 9
It can be seen that the dividend is a smaller number than the divisor. So, to solve the supplied fraction, we need a Decimal Point. If we place a zero to the right of the remainder, this is possible. As a result, we receive 70, which must now be divided by 9. Below is a description of the division’s steps:
70 $\div$ 9 $\approx$ 7
Where:
9 x 7 = 63
A Remainder is produced and is given as:
70 – 63 = 7
As we get a non-zero remainder, we once again add a zero to the right of the remainder, but this time without the insertion of a decimal point. So, the remainder of 7 becomes 70 again and we have to divide it by 9.
70 $\div$ 9 $\approx$ 7
Where:
9 x 7 = 63
To calculate the remainder, we proceed as follows:
70 – 63 = 7
We observe that both the Remainder and Quotient are the same as that obtained in the previous step. This illustrates that a given fraction is a non-terminating and recurring fraction. Thus, we don’t need to calculate further, and our final answer is 0.777 with a remainder of 7.
]Images/mathematical drawings are created with GeoGebra.
