What Is 2/7 as a Decimal + Solution With Free Steps
 The fraction 2/7 as a decimal is equal to 0.28571.
The fraction 2/7 as a decimal is equal to 0.28571.
Division is one of the mathematical operations used in solving mathematical problems. It can be solved in different ways depending upon the nature of the problem, but one of the most common and effective ways to solve problems related to division is Long Division.
To solve the fraction 2/7, the complete solution is given using the method called Long Division.
Solution
Before solving the problem, we have to understand the terms involved in the fraction. As a fraction is composed of a denominator and numerator, the denominator is referred to as the Divisor and the numerator is called a Dividend.
Dividend = 2
Divisor = 7
When we divide a fraction, the result we get is referred to as the Quotient.
Quotient = Dividend $\div$ Divisor = 2 $\div$ 7
The long division method result is as under for the desired fraction: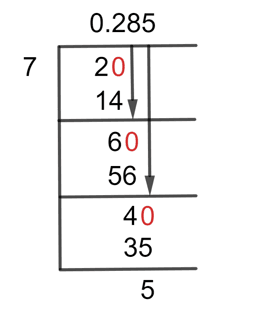
Figure 1
2/7 Long Division Method
You may examine the Long Division Method used to resolve this problem in more detail by carrying out the following actions.
So, the fraction we have is:
2 $\div$ 7
To proceed with this problem, first we have to add the decimal point because the numerator value is less than the denominator value because 2 is less than 7.
Another term is used while dealing with the problems related to division and that term is referred to as Remainder, which is the remaining part of the division after every step during the long division process.
Since 2 is a numerator here in this situation, so we will add Zero to its right, by doing so we get a number 20. So now, we determine:
20 $\div$ 7 $\approx$ 2
Where:
7 x 2 = 10
After doing this, we end up with the Remainder of 6 and we get this by 20 – 14 = 6.
After receiving a remainder from the division, we repeat the operation and add a Zero to the Remainder’s right. Now we don’t need to add another decimal point because the Quotient in this case already has a decimal value.
So by adding Zero to the previous remainder we now have 60 because the previous remainder was 6. The solution will proceed as follows:
60 $\div$ 7 $\approx$ 8
Where:
7 x 8 = 56
So after this step, we end up with the Remainder of 4. Now we will repeat the step used in the previous step of adding Zero to the right of the remainder and now the remainder becomes 40. This time there is no need to add the decimal point because it is already in the Quotient.
40 $\div$ 7 $\approx$ 5
Where:
7 x 5 = 35
So, after this step, we have a Remainder of 5 and the resulting Quotient is 0.285. To get a more accurate result we can further solve this.
Images/mathematical drawings are created with GeoGebra.
