What Is 2 7/8 as a Decimal + Solution With Free Steps

The fraction 2 7/8 as a decimal is equal to 2.875.
Generally, fractions are expressed in p/q form, where p and q represent the numerator and denominator of the fraction, respectively. The three classifications that apply to fractions are proper fractions, improper fractions, and mixed fractions.
A fraction that whose numerator is lesser than the denominator is considered to be a proper fraction. A fraction with a greater numerator is considered an improper fraction. Improper fractions and whole numbers are combined to form mixed fractions.
The given mixed fraction, 2 7/8, can be converted to its decimal value using the Long Division method. We convert fractions into decimals because decimal values are easier to understand and more useful in solving mathematical problems.
Solution
The mixed fractions can be easily converted into improper fractions by first multiplying the denominator of the fraction by the whole number and then adding the numerator to it while the denominator stays the same. The fraction we now have is 23/8 as a result.
The Dividend and the Divisor are two important terms used in the long division method. The denominator of the fraction is referred to as a “divisor,” whereas the fraction’s numerator is called a “dividend.” As a result, the given fraction has a dividend of 23 and a divisor of 8.
Dividend = 23
Divisor = 8
The result we get in decimal value after solving a fraction is known as the Quotient.
Quotient = Dividend $ \div $ Divisor = 23 $ \div $ 8
The following is the long division method for the given fraction of 23/8: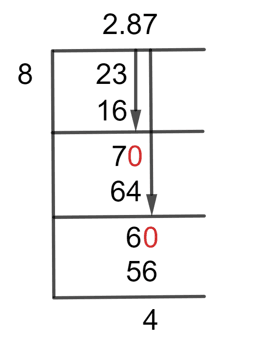
Figure 1
23/8 Long Division Method
The fraction we have is:
23 $ \div $ 8
In this case, the numerator is greater than the denominator. The two numbers are immediately divisible. As a result, we will have a quotient that is higher than one.
The number that remains after two non-equally divisible numbers are divided is known as the Remainder.
23 $ \div $ 8 $ \approx $ 2
Where:
8 x 2 = 16
This leaves us with a remainder of 7. These two numbers cannot be divided any further since the remainder is less than the divisor. So to proceed further, we need to multiply our remainder by ten, for which we will add a decimal point to the quotient.
So, after adding a decimal point and multiplying our remainder with ten, we now have a remainder of 70.
70 $ \div $ 8 $ \approx $ 8
Where:
8 x 8 = 64
The Remainder we have now is 70 – 64 = 6. Again, we have a case of remainder less than the divisor, so we will repeat the step of multiplying 10 with our remainder, so now the remainder becomes 60.
60 $ \div $ 8 $ \approx $ 7
Where:
8 x 7 = 56
After this step, we have a Remainder of 4 with a Quotient of 2.87. To get a more precise answer in decimal, we can solve it further.
Images/mathematical drawings are created with GeoGebra.
