What Is 8/25 as a Decimal + Solution With Free Steps

The fraction 8/25 as a decimal is equal to 0.32.
In the form of p/q, a fraction is an expression that can be used to indicate the relationship between two integers.
A Fraction is a name for the mathematical representation of something divided into two or more portions or parts. For example, the Denominator and the Numerator are the two parts of a fraction. Usually, solving fractions using multiples other than their fractional representations is difficult. But turning them into division is a simple solution.
Instead of using the Multiples method in this case, we solve these fractions using the Long Division method. Finally, we receive the outcome using this method in decimal values.
So here, we are using the Long division method to find the decimal equivalent of the fraction 8/25 in this problem.
Solution
The Dividend, which is being divided, and the Divisor, which is the number performing the dividing, are the first two parts of our fraction that we shall dissect. The procedure is as follows:
Dividend = 8
Divisor = 25
Quotient and Remainder are two more division-specific terminologies that might be used. The result of dividing is the solution or Quotient.
It can be stated as follows:
Quotient = Dividend $\div$ Divisor = 8 $\div$ 25
The Remainder, on the other hand, stands for a term that is left over after partial division. And the remainder is also used as a dividend for upcoming iterations in the division.
Let’s get into the Long Division solution of our fraction 8/25 as we are using this technique to solve this division:
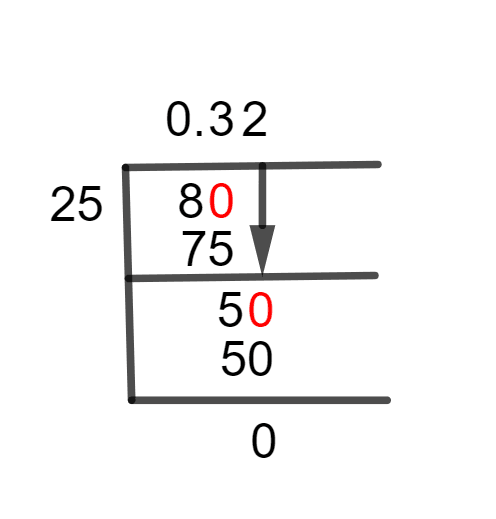
Figure 1
8/25 Long Division Method
The first step in applying the long division method to solve a fraction is to represent the fraction as a division:
8 $\div$ 25
First, determining if the Dividend is greater than the Divisor is the first step in long division. We have to use a decimal point if the divisor is greater. We must add a zero to the dividend’s right to achieve this. If the dividend is greater, we can omit the decimal point.
In the above scenario, 8 is smaller than 25, which means the Divisor is smaller than the Dividend. Hence we require a Decimal Point to proceed.
So next, add a 0 to the dividend and a decimal to the quotient as follows:
80 $\div$ 25 $\approx$ 3
Where:
25 x 3 = 75
To determine the Remainder, subtract the two values given below:
80 – 75 =5
As a remainder 5 is obtained, the procedure is repeated by adding zero to dividends right and making it 50:
50 $\div$ 25 = 2
Where:
25 x 2 = 50
Reminder:
25 – 25 = 0
As a result of this division, we have 0 remainders. Therefore, it signifies that the fraction has been completely solved and that no more operations are required. As a result, we have a Quotient of 0.32 with no remainder.
Images/mathematical drawings are created with GeoGebra.
