What Is 5 1/4 as a Decimal + Solution With Free Steps

The fraction 5 1/4 as a decimal is equal to 5.2.
A Fraction can be employed to separate a smaller portion from a more extensive or complete object. For instance, the fraction 1/8 represents the eighth part of any item. These are also useful in estimating how many components of similar sizes can be combined to obtain a whole object.
According to the respective sizes of the numerator and denominator, the fraction might be either a Proper, Improper, or Mixed fraction. We refer to the combination of a proper fraction and a whole number as a mixed fraction. An example is 5 1/4 containing 5 as a whole number and 1/4 as a proper fraction.
Among the different methods to solve a fraction, one is the Long Division method. It gives us the decimal value and will be studied in detail here.
Solution
Since we have a mixed fraction to solve, we cannot solve it until it is transformed into an improper fraction. The equivalent improper fraction is determined as 21/4.
This fraction will now be solved by division. A division problem has three main elements: dividend, divisor, and quotient. Any number divided into smaller portions is called a Dividend, while the dividing number is termed a Divisor. However, the number obtained as an answer after dividing two numbers is called a Quotient.
The fraction of 21/4 has the following components.
Dividend = 21
Divisor = 4
Quotient = Dividend $\div$ Divisor = 21 $\div$ 4
Another term associated with the Division process is remainder. Sometimes, we have two numbers that cannot be divided evenly. These numbers give us certain left-over along with the quotient, which is referred to as Remainder.
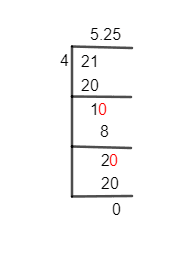
Figure 1
5 1/4 Long Division Method
Long Division in mathematics is a methodology for breaking down complex division problems into a series of simpler and smaller steps. As an example, the solution of 21/4 is mentioned here.
21 $\div$ 4
A greater dividend than a divisor indicates that at this point, we can move forward without a Decimal Point. Thus, the division of 21 by 4 is mathematically stated as:
21 $\div$ 4 \approx 5
4 \times 5 = 20
1 is acquired as the value which is left behind.
21 – 20 = 1
This remaining value 1 is made 10, and a decimal point is gotten in the Quotient. Thus, the division is continued as follows.
10 $\div$ 4 \approx 2
4 \times 2 = 8
Deduction of 8 from 10 gives us 2 as the remaining value.
10 – 8 = 2
This 2 is changed to 20 and divided by 4.
20 $\div$ 4 = 5
4 \times 5 = 20
There is no remaining value in this step.
20 – 20 =0
Hence, we have 5.25 as the determined decimal value of 5 1/4.

Images/mathematical drawings are created with GeoGebra.
