What Is 5/10 as a Decimal + Solution With Free Steps

The fraction 5/10 as a decimal is equal to 0.5.
Fractions are proportions of numbers. They are expressed as a ratio of one number to another. The bottom part, the Denominator, tells you how many parts the whole is divided into, and the top part, the Numerator, means you how many you have.
But because this fractional representation limits the use of multiples to solve these divisions, so we use the long division method.
We often feel the urge to convert fractions to decimals because it helps us understand fractions. Moreover, it is simple to determine which of two decimal values is greater and which is smaller when comparing them. When we compare fractions with different numerators and denominators, however, the outcomes are not always clear.
In this example, we will use the Long Division method to convert a fraction of 5/10 to a decimal.
Solution
The first step in solving a fraction is determining whether it is a proper fraction or an improper fraction. A Proper Fraction is the one in which the numerator is smaller than the denominator. And Improper Fraction is one in which the numerator is greater than the denominator.
During the division process when we did a conversion of the fraction into division. We classified its components based on how they function. The numerator is represented as the Dividend, and it is divided by the denominator, also known as the Divisor. In the fraction, we can thus see them extracted as follows:
Dividend = 5
Divisor = 10
Now we introduce another concept, the Quotient, which is the resulting answer to a division, which may be represented typically as:
Quotient = Dividend $\div$ Divisor = 5 $\div$ 10
The Quotient is the final result achieved after completing the division procedure. The Quotient is what we’re looking for in the provided fraction, and it’s significantly influenced by the dividend and divisor. As can be seen, our dividend of 5 is less than the divisor’s 10, resulting in a Quotient with a whole number of 0.
Now, using the Long Division Method, we solve our problem as follows:
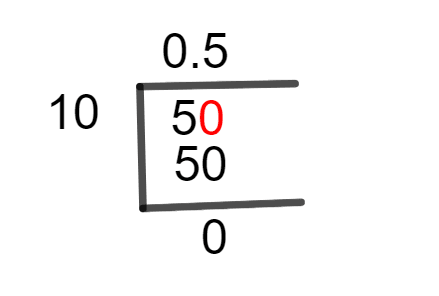
Figure 1
5/10 Long Division Method
The given fraction is:
5 $\div$ 10
The first step in solving a Long division is to determine if the provided fraction is proper or improper. If it’s a Proper fraction, we’ll need a Decimal Point, by inserting zero to the right side of dividend.
In our case, a proper fraction is given so by inserting a zero to the right of 5, we get 50, which may now be divided by 10, as seen below:
50 $\div$ 10 $\approx$ 5
Where:
5 x 10 = 50
This produces a Remainder equal to:
50 – 50 = 0
The value that is left after an incomplete division is known as the Remainder.
We don’t need to evaluate anymore because we have 0 as the Remainder and the Quotient of this fraction is 0.5.
Images/mathematical drawings are created with GeoGebra.
3 1/4 As A Decimal | Fractions to Decimals List | 11/12 As A Decimal
