What Is 5/11 as a Decimal + Solution With Free Steps

The fraction 5/11 as a decimal is equal to 0.45454545454.
Fractions have a numerator and a denominator and are represented in p/q form. The p and q represent the numerator and denominator, respectively. We convert fractions to decimal values to make them easier to understand, and this conversion requires a mathematical operation called division.
Division seems difficult among all mathematical operators, but actually, it is not. We can convert fractions to their decimal value by using a method called the Long Division method. For the given fraction of 5/11, we can use the long division method to get its decimal value.
Solution
Before finding the solution through the long division method, there is a need to understand important terms. Important terms are “Dividend” and “Divisor.” The numerator in the fraction is known as the dividend, and the denominator is referred to as the divisor. If we talk about the p/q form, then the p in the fraction is referred to as the dividend while the q is known as the divisor.
For the given fraction of 5/11, the dividend and the divisor are:
Dividend = 5
Divisor = 11
There is a need to understand another important term which is Quotient. It is the result of the fraction in the decimal value after the solution to the long division method.
Quotient = Dividend $ \div $ Divisor = 5 $ \div $ 11
The solution to the fraction through long division is as under: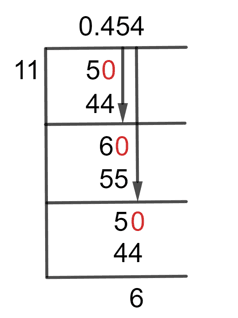
Figure 1
5/11 Long Division Method
We have:
5 $ \div $ 11
Here, we have a numerator of 5 and the denominator of the given fraction is 11. It can be seen that we cannot divide these numbers directly because the numerator is less than the denominator.
So we need to add zero to the right side of the dividend to proceed to our solution. For that, we have to add the decimal point to the quotient. After doing this now, we have a dividend of 50.
When two numbers are not completely divisible by each other, the leftover number is referred to as the remainder. So now we have:
50 $ \div $ 11 $ \approx $ 4
Where:
11 x 4 = 44
The remainder we have is 6. Again, we are in a situation where the remainder is less than the divisor, so we will add zero to the right side of the remainder, and this time there is no need to add the decimal point to the quotient because it is already in the quotient.
So by doing this, we have a remainder of 60.
60 $ \div $ 11 $ \approx $ 5
Where:
11 x 5 = 55
After this step, we got a remainder of 5. Again, by putting zero to the remainder right, we have a remainder of 50.
50 $ \div $ 11 $ \approx $ 4
Where:
11 x 4 = 44
So we have a resulting Quotient of 0.454 with a Remainder of 6.
Images/mathematical drawings are created with GeoGebra.
