What Is 5/4 as a Decimal + Solution With Free Steps
 The fraction 5/4 as a decimal is equal to 1.25.
The fraction 5/4 as a decimal is equal to 1.25.
Division is one of the difficult operations in mathematical problems and when it comes to fraction base division it becomes complicated for most people, but here is a method called Long Division through which fractions can be solved quite easily.
The detailed solution by using the Long Division method for the given fraction 5/4 is provided in this guide.
Solution
The two important terms use in this method are Dividend and Divisor. The numerator of the fraction is known as the Dividend and the denominator is called as Divisor. In this fraction, 5 is the Dividend, and 4 is the Divisor.
Dividend = 5
Divisor = 4
The resulting term through this process is referred to as Quotient.
Quotient = Dividend $\div$ Divisor = 5 $\div$ 4
Now, by using the method called Long Division, the fraction can be solved as follows: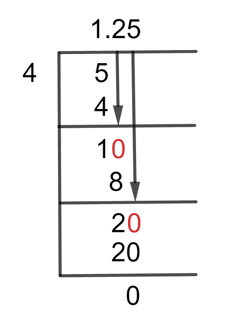
Figure 1
5/4 Long Division Method
Here is the step-by-step approach to solving the given fraction using the Long Division method.
We have a fraction:
5 $\div$ 4
Here, we know that the numerator is greater than the denominator so we can directly divide both terms.
There is a need for an important term to be introduced named a Remainder. It is the leftover part after the division of two numbers in the Long Division method.
5 $\div$ 4 $\approx$ 1
Where:
4 x 1 = 4
After this step, the Remainder we have is 1. Now it can be seen that we cannot proceed with the further division because the remainder is less than the Divisor, so we have to add the Decimal point to the Quotient.
After adding the decimal point to the Quotient we can now multiply our remainder by 10 and after doing so our new Remainder is 10. Now the further solution to this problem is:
10 $\div$ 4 $\approx$ 2
Where:
4 x 2 = 8
After this step, we now have a Remainder of 2. As of now, the remainder is again less than the divisor, so for the further process, we have to multiply this term by 10. By doing so, the remainder we now have is 20. This time, there is no need to add the Decimal point because the decimal point is already added in the previous step, and in the Long division process, we only add the decimal point once, after that we just add zeros to the Remainder’s right and proceed with the solution.
20 $\div$ 4 = 5
Where:
4 x 5 = 20
So, after this step now we have a Remainder of 0 means this is the exact solution of the fraction. Therefore, the resulting Quotient is 1.25 for the fraction of 5/4.
Images/mathematical drawings are created with GeoGebra.
