What Is 5/8 as a Decimal + Solution With Free Steps
 The fraction 5/8 as a decimal is equal to 0.625.
The fraction 5/8 as a decimal is equal to 0.625.
Division in mathematics is the process of splitting a number into equal parts and figuring out how many equal parts there are. Usually, division appears to be more complicated compared to other mathematical operations.
But there is a method to solve this seemingly difficult operation that makes it easy. The technique used to solve the given question is Long Division.
The mathematical procedure for splitting big numbers into smaller groups or pieces is known as long division. It is beneficial to simplify complex issues.
The given fraction of 5/8 will be solved here by the Long Division method to get its decimal equivalent.
Solution
To solve a fraction first, its components are separated based on their operations. While dividing, the number which is to be divided is represented as a Dividend, whereas a Divisor represents a number that divides the dividend. In the given problem, the dividend is 5 and the divisor is 8.
After the complete division of a fraction, we get a Quotient that can be defined as the result of the division and a Remainder that represents the remaining value obtained due to incomplete division. In the given problem, we have:
Dividend = 5
Divisor = 8
Quotient = Dividend $\div$ Divisor = 5 $\div$ 8
It can now be solved by the method of Long Division.
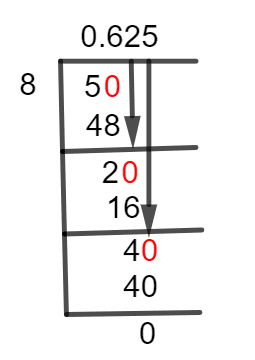
Figure 1
5/8 Long Division Method
Now we apply the technique of Long Division to solve this fraction.
We are given in the problem:
5 $\div$ 8
Here, 5 is the dividend, and 8 is the divisor. As 5 is less than 8, so we need a Decimal Point to solve this fraction. For this purpose, we have to place a zero to the right of the Remainder, which is 5 in this case. After placing the zero, it becomes 50. Then we solve as:
50 $\div$ 8 $\approx$ 6
Where:
8 x 6 = 48
It shows that a Remainder is produced in the result, which is equivalent to:
50 – 48 = 2
Since there is a remainder produced, we once more add a zero to the right of the remainder, but this time without the decimal point. Because the decimal value of Quotient already exists. Thus, we get 20 after inserting zero to the remainder’s right. Further calculations are done as:
20 $\div$ 8 $\approx$ 2
Where:
8 x 2 = 16
Now, we get 4 as a remainder, which becomes 40 after inserting another zero. Further computations can then be done as:
40 $\div$ 8 $\approx$ 5
Where:
8 x 5 = 40
This time, we get the value of Quotient as 0.625 and Remainder as 0. This shows that no more calculations are needed and this is the accurate result of this division.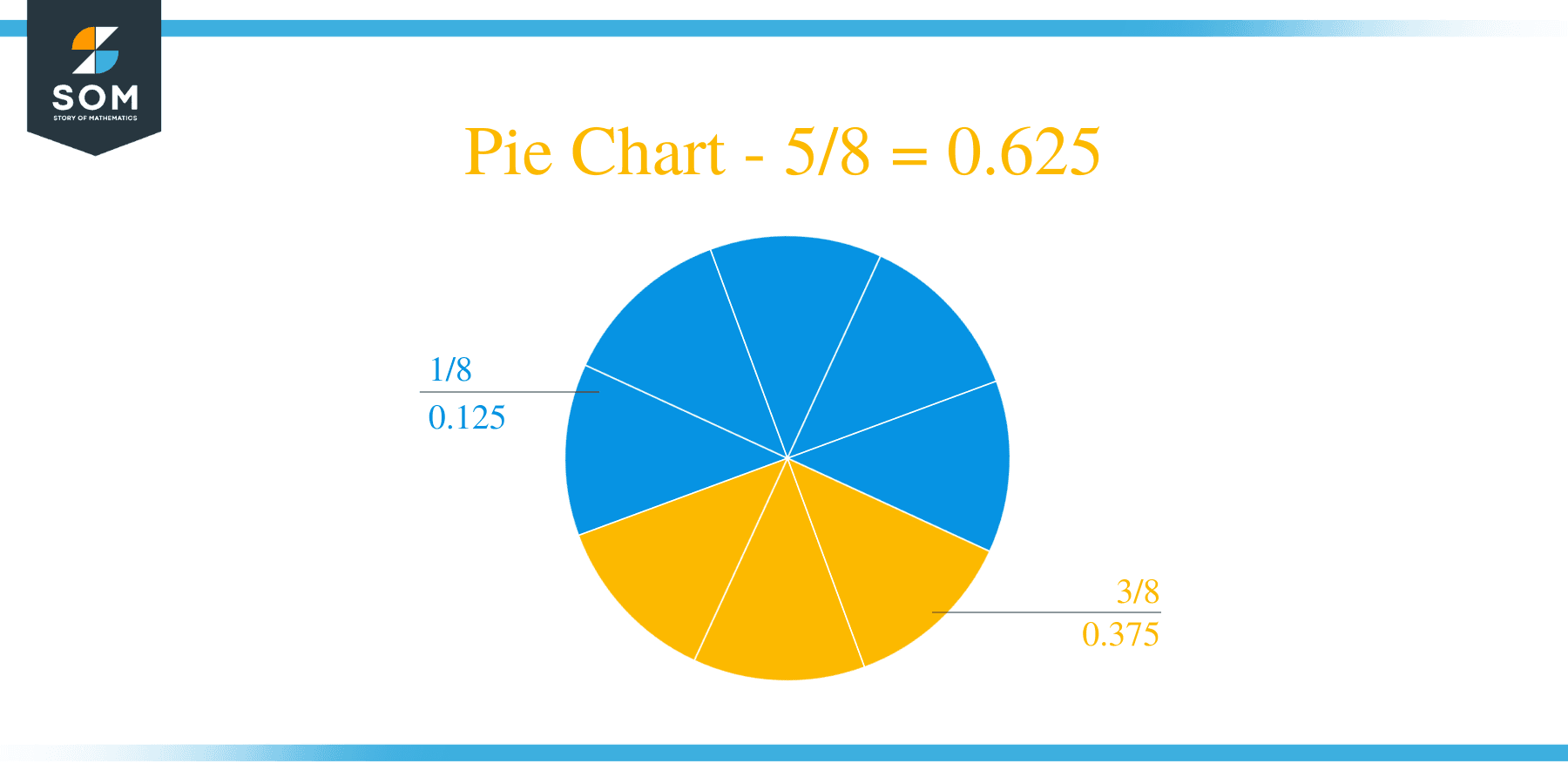
Images/mathematical drawings are created with GeoGebra.
