What Is 6/10 as a Decimal + Solution With Free Steps
 The fraction 6/10 as a decimal is equal to 0.6.
The fraction 6/10 as a decimal is equal to 0.6.
We know that there are four basic Mathematical Operations on which most mathematical calculations are based. One of these is the division, and it is expressed between two numbers as p/q. This expression is therefore called a Fraction.
Where p/q is a fraction of the size q for the number p. So, Fractions are used to express divisions that cannot be solved using traditional multiplication methods.
Now, divisions of the such sort which cannot be solved beyond a certain point that they have to be expressed in terms of a Fraction can be solved to result in a Decimal Value.
Let’s go through the solution to our problem at hand on 6/10.
Solution
A fraction is composed of two numbers, one which is divided and the other which divides, and these are known as the Dividend and the Divisor, respectively. Now, identifying these components is very important:
Dividend = 6
Divisor = 10
Here, we will introduce the term Quotient which refers to the solution of a division. A Quotient is completely dependent on the numbers Dividend and the Divisor. The very nature of the Quotient can be extracted by just comparing these numbers.
It is a rule of thumb that a dividend smaller than the divisor will always result in a Quotient smaller than 1 and vice versa.
Quotient = Dividend $\div$ Divisor = 6 $\div$ 10
Now, to find this Quotient for numbers that do not divide completely we use a special method, this is called the Long Division Method. Let’s look at the Long Division solution of our fraction 6/10:
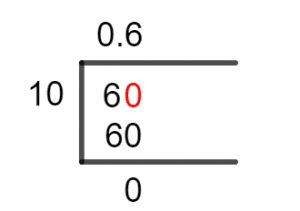
Figure 1
6/10 Long Division Method
Before we begin to solve a fraction into a division, we start by expressing a said fraction in the form of a division:
6 $\div$ 10
Now, we will introduce the final and one of the most significant quantities we will be dealing with here, the Remainder. A Remainder is a number that is produced as a result of an incomplete division, a division where the divisor is not a factor of the dividend.
Under such circumstances, the divisor is used to find the Multiple which is the closest to the dividend but also Smaller. This is how the quotient is solved in Iterations of incomplete divisions.
We begin by analyzing the dividend of 6 which is smaller than the divisor of 10, so we shall introduce a Zero to the right of 6. This will produce 60 as our dividend.
60 $\div$ 10 = 6
Where:
10 x 6 = 60
Hence, no remainder is produced, but the Quotient needs compilation. As we know the Quotient for the division 60/10 is 6 but not for the fraction 6/10.
The addition of Zero to the right of 6 came at an addition of a Decimal Point to the Quotient. Therefore, our Quotient has become:
6 $\div$ 10 = 0.6
Images/mathematical drawings are created with GeoGebra.
