What Is 9/20 as a Decimal + Solution With Free Steps
 The fraction 9/20 as a decimal is equal to 0.45.
The fraction 9/20 as a decimal is equal to 0.45.
Fraction is an expression to represent the ratio of two whole numbers as p/q. It denotes the proportion of p pieces to the total q pieces. A fraction consists of two components: the numerator and denominator, distinguished by a line between them.
Numerator P is a number above the line, while the Denominator q is a number below the line. The line between them represents the process of Division.
Thus, a fraction can be e solved by division to obtain its equivalent decimal number, which is considered to be a complex process.
An example is presented here, to solve a fraction of 9/20 by the Long Division method.
Solution
A fraction has to be converted into a division to get its solution. This can be done by separating its elements based on their functions.
Thus, the numerator, which has to be divided is represented as the Dividend, and the denominator, which is dividing the numerator, is described as the Divisor. In the given fraction of 9/20, 9 is the dividend, and 20 is the divisor.
Mathematically, it can be written as:
Dividend = 9
Divisor = 20
The other two important division-specific terms, which are necessary to understand, are Quotient and Remainder. A quotient is defined as the final result obtained by the division of two numbers. On the other hand, the remainder is a left-over value due to incomplete or partial division.
Quotient = Dividend $\div$ Divisor = 9 $\div$ 20
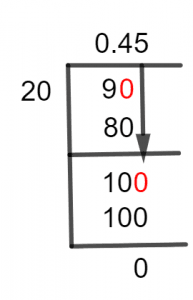
Figure 1
9/20 Long Division Method
The complete solution of 9/20 using the Long Division method is shown below.
9 $\div$ 20
To get the solution of a fraction, we must first determine the greater number among the numerator and the denominator. If the numerator is a bigger number than the denominator, a Decimal Point is needed for the solution. So, we place a zero to the dividend’s right and insert a decimal point in the final answer. In this case, after inserting a zero to the right of 9, we get 90.
Now, 90 has to be divided by 20.
90 $\div$ 20 $\approx$ 4
Where:
20 x 4 = 80
We get 10 as the remainder as shown below:
90 – 80 = 10
This non-zero value of the remainder indicates that we again have to insert a zero to its right. But this time, the decimal point is not required. By the insertion of zero, we get 100 to divide by 20.
100 $\div$ 20 $\approx$ 5
Where:
20 x 5 = 100
The remainder is given as:
100 – 100 = 0
Since 100 is a multiple of 20, so we have a zero Remainder. This tells us that the divisor is a factor of dividend and the Quotient 0.45 is the decimal value of the fraction.
Images/mathematical drawings are created with GeoGebra.
