Add|Definition & Meaning

Adding is the process of combining two or more items. In mathematics, the process of calculating two or more numbers is called adding. It is an essential arithmetic operation that we all use daily.  

Figure 1 shows that 5 blue circles are added with 2 red circles and produce 7 circles. 

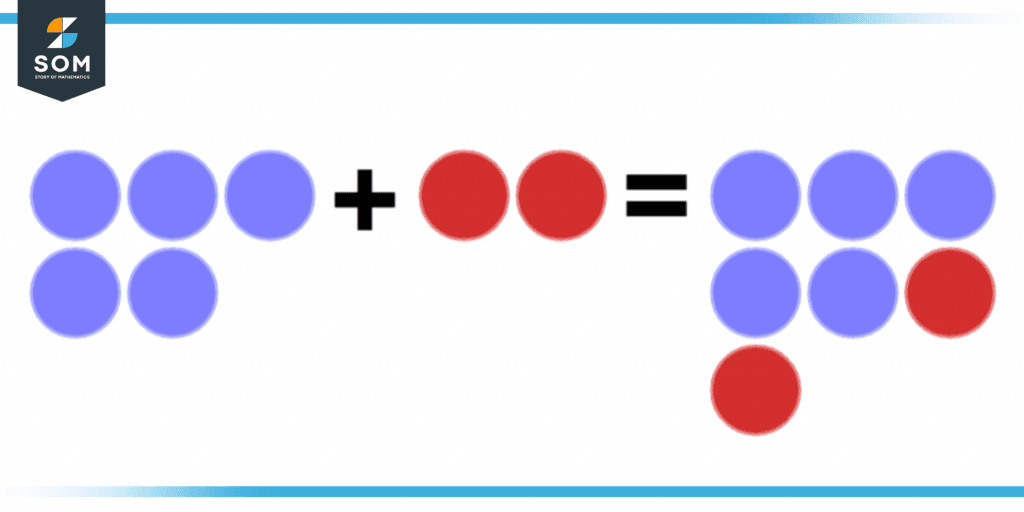
Figure 1 – Example of addition of circles.

Parts of Addition

• Addend: The addends are the numbers that are added together.
• Addition Symbol: One of the standard mathematical symbols is the addition symbol. The plus sign (+) between the addends denotes addition. The equal to sign (=) is placed just before the sum is written in a statement that is written horizontally, as shown below.
• Sum: The sum is the final result reached after adding the addends.

We use these parts to create a formula to add numbers together. The formula looks something like this addend + addend = sum. 

Properties of Adding 

We need to remember three primary properties when adding two numbers together.

• Commutative Property: It means that altering the placement or order of two numbers while adding them will not affect the outcome. As an example, 6 + 2 equals 8, and 2 + 6 equals 8. The sum of two numbers is independent of the order in which they are added.
• Associative Property: With the associative property of addition, we can arrange the numbers in any way we like when adding three or more of them. No matter how we arrange them, the sum is the same. For example, the sum of (2 + 3) + 5 is 10 and the sum of 2 + (3 + 5) = 10 is also 10.
• Additive Identity Property: This property is applied when numbers are added to zero. In this property, zero is known as the identity element. As a result, if we add any number to zero, the result will be the same number. This property applies to complex numbers, real numbers, rational numbers, integers, and other numbers. 

Additional Information About Adding

When adding two numbers, one-digit numbers can be added simply, but for larger numbers, we divide them into columns based on their respective place values, such as ones, tens, hundreds, thousands, and so on.

According to the place value system, we always begin addition on the right side. This means that we start with the one’s column, proceed to the tens column, then the hundreds column, and so on. While working on such problems, we may encounter cases with and without carry-overs.

Let’s look at how we can add large numbers with and without regrouping.

Adding Without Regrouping

 For example, we have 125 and add this number to 350. We will start with the first column and add 5 and 0, which gives us 5. We then move towards the tens column and add 2 and 5, which provides us with 7.

Finally, we move towards the hundreds column and add 1 and 3, which gives us 4. The total sum of the two numbers would be equal to 475. This is an example of adding numbers without regrouping.

Adding With Regrouping

When we are adding numbers, if the sum of the addends in any of the columns is greater than 9, we regroup this sum into tens and ones. The tens digit of the sum is then carried over to the preceding column, and the one’s number of the sum is written in that column.

For example, we have two numbers, 145 and 135, and we add them together. We will start with the first column, where 5 and 5 are added together.

The sum of the first column is 10; we carry the 1 from the 10 and add it in the tenth column; we only write the 0. When we move into the tenth column, we add the numbers 4 and 3 along with the carried 1 from the one’s column.

This gives us 8. In the hundreds column, we add the numbers 1 and 1 to get 2. After combining the results, we get a sum of 280.

Representing How Adding Is Done

We can display the concept of adding by using the following figures:

Figure 2 below shows 2 green circles, 5 blue circles, and 2 red circles. When all these circles are added together, the sum is 9 circles.

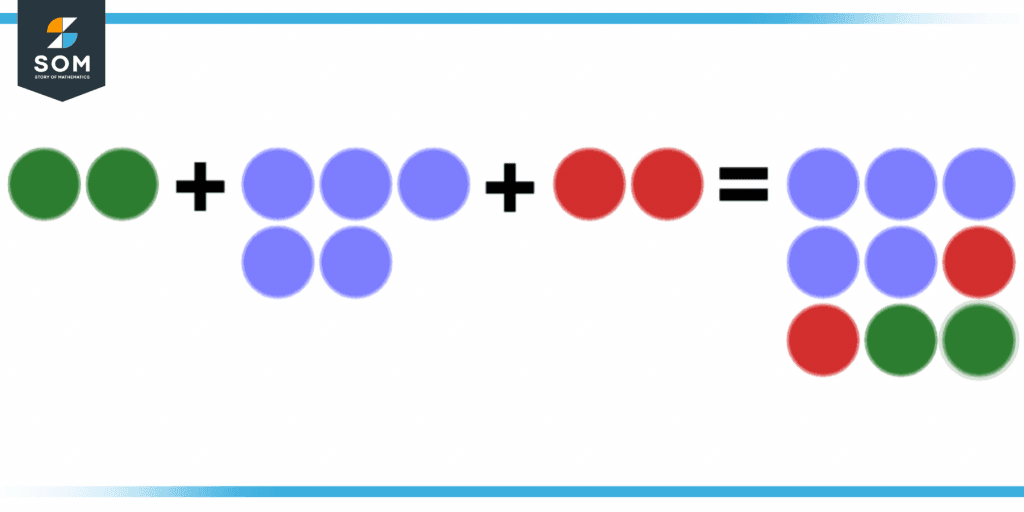
Figure 2 – Illustration representing addition.

Figure 3 also clearly shows the concept of adding numbers or items together, as seen below:

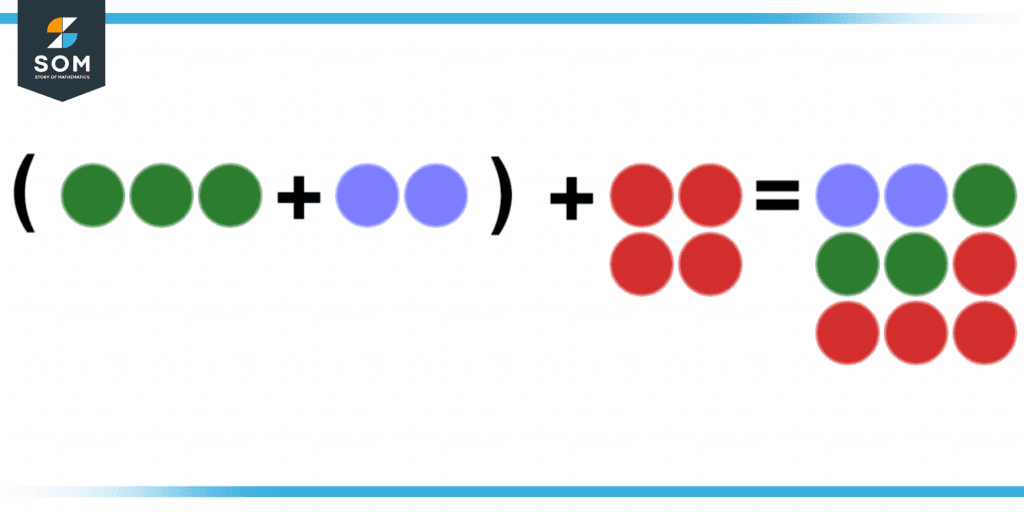
Figure 3 – Addition method with brackets.

The figure above shows that despite how the numbers are added, they produce the same outcome. The figure shows 3 green circles and 2 blue circles added first, and then 4 circles are added to their sum. The answer is still the same 9 circles.

Figure 4 also shows how 4 blue boxes, when added with 3 red square boxes, give us 7 boxes.

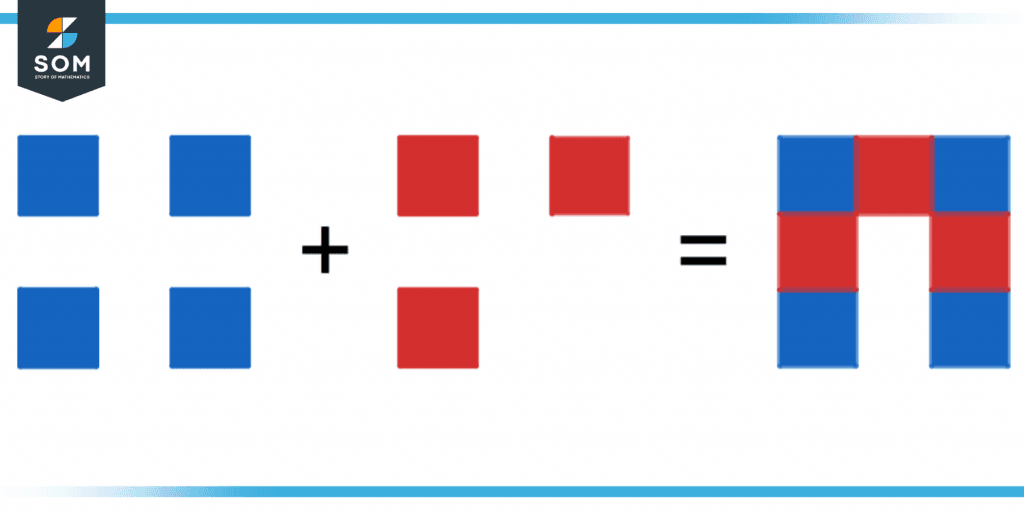
Figure 4 – Addition with squares.

An Example of Adding Numbers

During the baseball game, the number of viewers in the first row of the stadium is 235. The number of viewers in the second row is 300, and the number of spectators in the third row is 350. Find the total number of spectators in the game.

Solution

To find the total number of spectators in the baseball stadium, we need to add all the spectators from each row. When computing the total number, we get the following formula:

235 + 300 + 250

First, we add the first two addends to each other; that are 235 and 300. First, we solve the one’s column, add 5 and 0, and get a sum of 5. We then add the ten’s columns, 3 and 0, and get 3. Now adding the hundred’s column, add 1 and 5, which gives a sum of 5. Putting together all the numbers, we get 535. 

After adding the first two numbers, we take that outcome and add it with the last value. So the number we now add are 535 and 250. We repeat the previous process and start with the one’s column, we add the numbers 5 and 0, and the result is 5. We then add the numbers in the ten’s column, which are 3 and 5; the sum we get is 8. Now we add the hundred’s column, 5 and 2, and the sum is 7.

Finally, after combining all the numbers, we get a total of 785. This is the total number of spectators at the baseball game.

All images/tables are created using GeoGebra.

Acute Angle Definition < Glossary Index > Addend Definition