Addend|Definition & Meaning

Consider two numbers or quantities A and B on which the addition operation is performed as shown in figure 1. Both add up together to obtain a result S. 

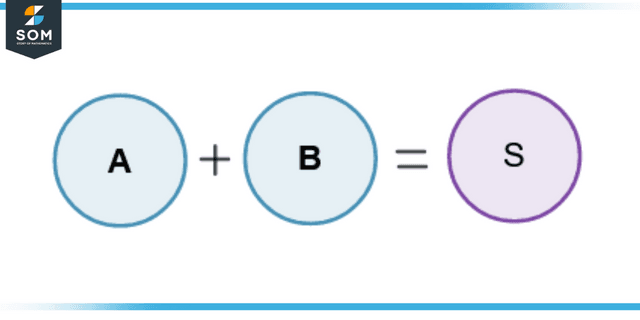
Figure 1 – Addition of two Addends A and B

Here, A and B are addends on the left-hand side and S is the sum or the total.

Origin of Addend

Addend comes from the Latin word “addendum, ” meaning to be added. An addend is also known as a summand. The word “summand” includes the word “sum” which is the result obtained after the addition process.

For example, in the equation given below:

3 + 6 + 9 = 18

The numbers 3, 6, and 9 are called the addends or the summands as they are being added together and the result 18 is known as the sum.

Summands and Augends

The addends add up to give the sum thus the addends can also be referred to as the summands. Addends can be any numbers such as rational, irrational, integers, complex, and imaginary numbers that are being added together.

Addends can also be variables such as x and y on which the addition process is taking place. The addend which comes first while writing an addition equation is known as the “augend”.

Illustrations of Addend Through Different Properties of Addition

The concept of addition is a major concept that provides the basis for many other operations in mathematics. Addends play a key role to understand the process of addition.

The concept of addends is also explained through the commutative property of addition, the associative property of addition, and the additive identity.

Commutative Property of Addition

Consider figure 2 in which the addends are explained through the commutative property of addition. The commutative property states that the addition of addends will give the same result regardless of their position.

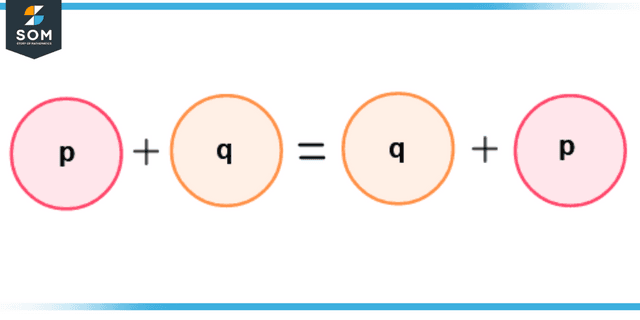
Figure 2 – Commutative Property of Addition showing Two Addends p and q

So, the addition of p and q will be equal to the addition of q and p according to the commutative property. Here, p and q are addends on both sides.

Associative Property of Addition

The associative property of addition consists of three addends that are added together. It states that any two addends can be added first and then added to the third addend. The addends l,m, and n are shown in figure 3.

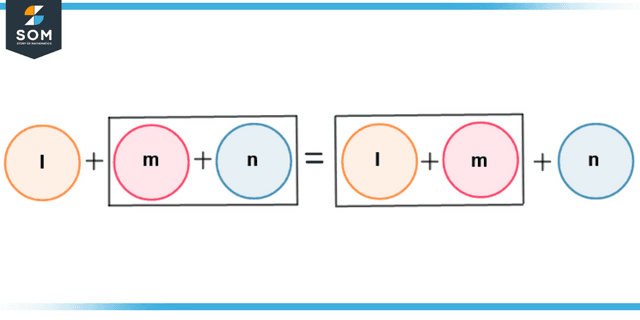
Figure 3 – Associative Property of Addition showing Three Addends

Additive Identity

The additive identity 0 is also an addend when added to any other number. It is called the additive identity as it keeps the identity of the number when added to it. Figure 4 shows the additive identity and another addend g.

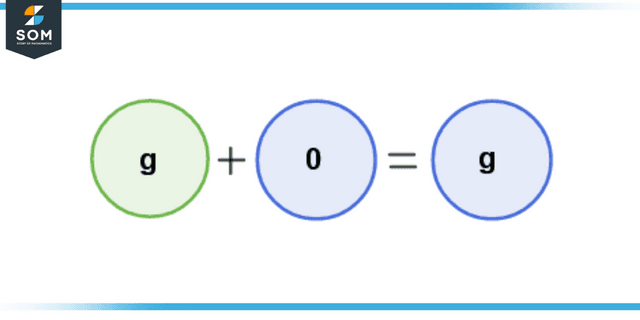
Figure 4 – Addition of the Additive Identity 0 and the Addend g

Use of Addends in Physics and Chemistry

Addend was first used in the 1900s when scientists explored the different fields of science. All fields of science include the process of addition as it is the most basic process.

The term “addend” is not restricted to numbers but can be any physical quantities that are being added together.

For example, in physics, the law of vector addition consists of two addends u and v which are vector quantities. The two vectors are added together to get a resultant sum of the two.

For example, in the field of chemistry, a chemical reaction requires two or more reactants which add up to give a product and some other by-products. The reactants are also referred to as addends as they are being added together chemically.

The chemical reaction of hydrogen and oxygen produces water. In this reaction, hydrogen and water are the addends.

Use of Addends in Daily Life

Addends are also used in our daily life. For example, when preparing a dish, the ingredients we add to the pot are also known as the addends. They can also be expressed as a mathematical expression through the addition operator.

Addends Not Having a Sum

The addition operation can only be learned efficiently if the addends are understood correctly. Sometimes, there are such addends which cannot produce a sum but are still called addends.

For example, adding a real number and an imaginary number cannot produce a sum but are still addends as both are being added together. Similarly, in the mathematical expression given below:

3xy + 2yz

The two terms cannot be added as they contain a different set of variables multiplied with them. But are still the addends as the addition operator joins them.

Finding a Missing Addend

A missing addend can also be calculated if the sum is known. The calculation of addends can also be useful in learning the subtraction process. An addend subtracted from the sum gives the other addend which was unknown.

Different addends can add to give the same sum or total. For example, the addends 5,5,5, and 2,7,6 add up to give the same sum of 15.

Examples

Example 1 – Identifying Addends

What are the addends in the following equation?

2 + 9 + 6 + 3 = 20

Solution

The addends in the given equation are 2,9,6, and 3 as they are the elements being added to provide the sum 20.

Example 2 – Finding the Missing Addend

Find the missing addend in the equation given below:

5 + 9 +13 + _ = 30

Solution

In order to find the missing addend in the given equation, the known addends should be added together to get the temporary sum as follows:

Temporary Sum = 5 + 9 + 13 = 27

The temporary sum 27 should be subtracted from the given sum 30 to get the missing addend in the equation. The equation will be:

Missing Addend = 30 – 27 = 3

So, the missing addend which completes the sum is 3.

Example 3 – Addends in a Chemical Reaction

A chemical reaction takes place between carbon and oxygen to produce carbon dioxide. What are the addends in this chemical reaction?

Solution

As carbon and oxygen are chemically mixed or added to form carbon dioxide, carbon and oxygen are the addends. Carbon dioxide is the product.

All the geometrical figures are created using GeoGebra.

Add Definition < Glossary Index > Addition Definition