Addition|Definition & Meaning

In simple words, addition is the process of adding something to get the total sum. Out of four fundamental arithmetic operations (addition, subtraction, multiplication, division) in mathematics, the addition operator is the most basic one.  

Graphical Demonstration

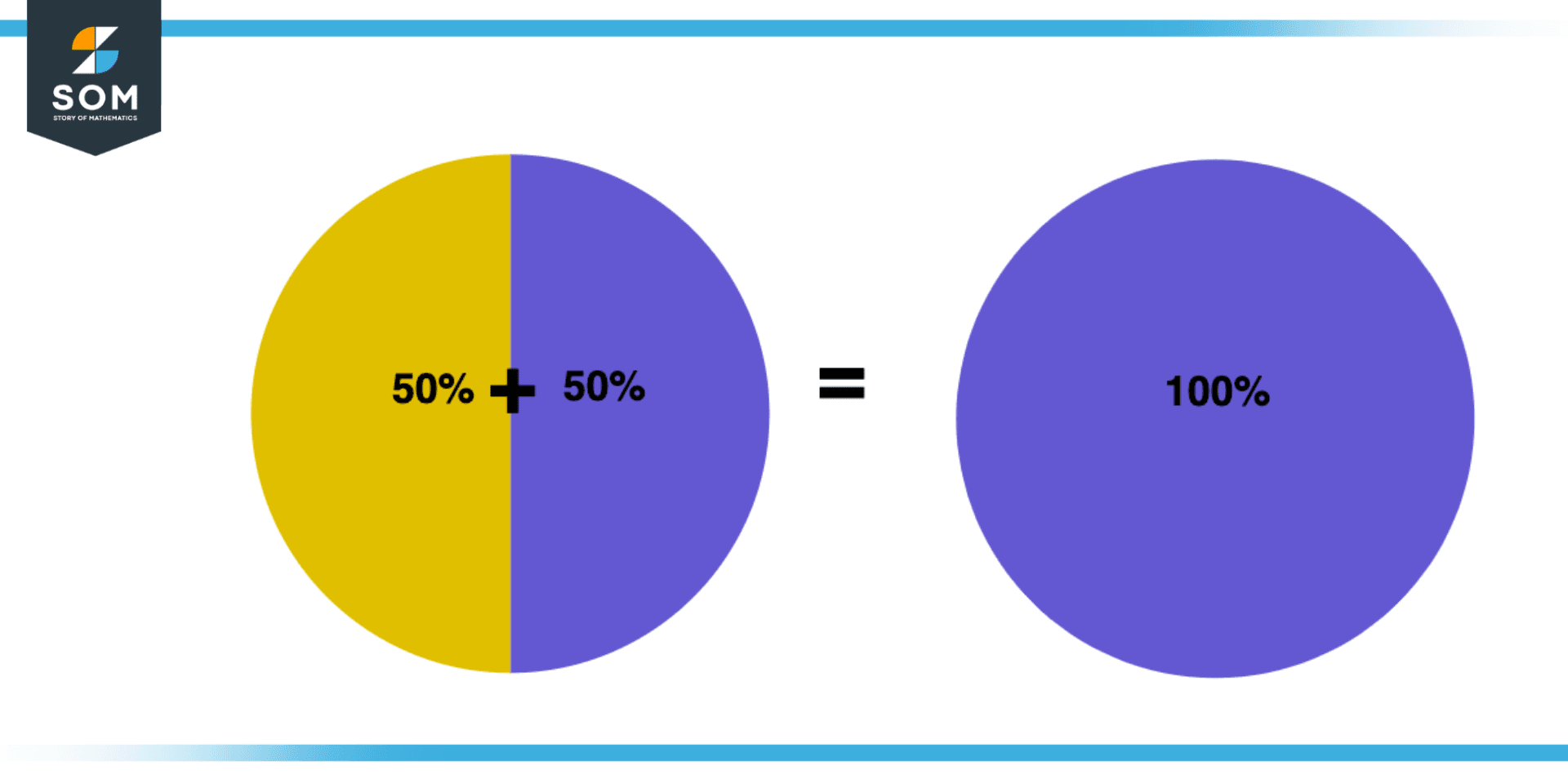
Figure 1 – Adding Sector of a Circle

Consider the above figure which represents the addition of sectors the pie is divided into two portions, the first portion represents 50% and the second portion represents 50% as well. Upon adding both we get a total of 100%.

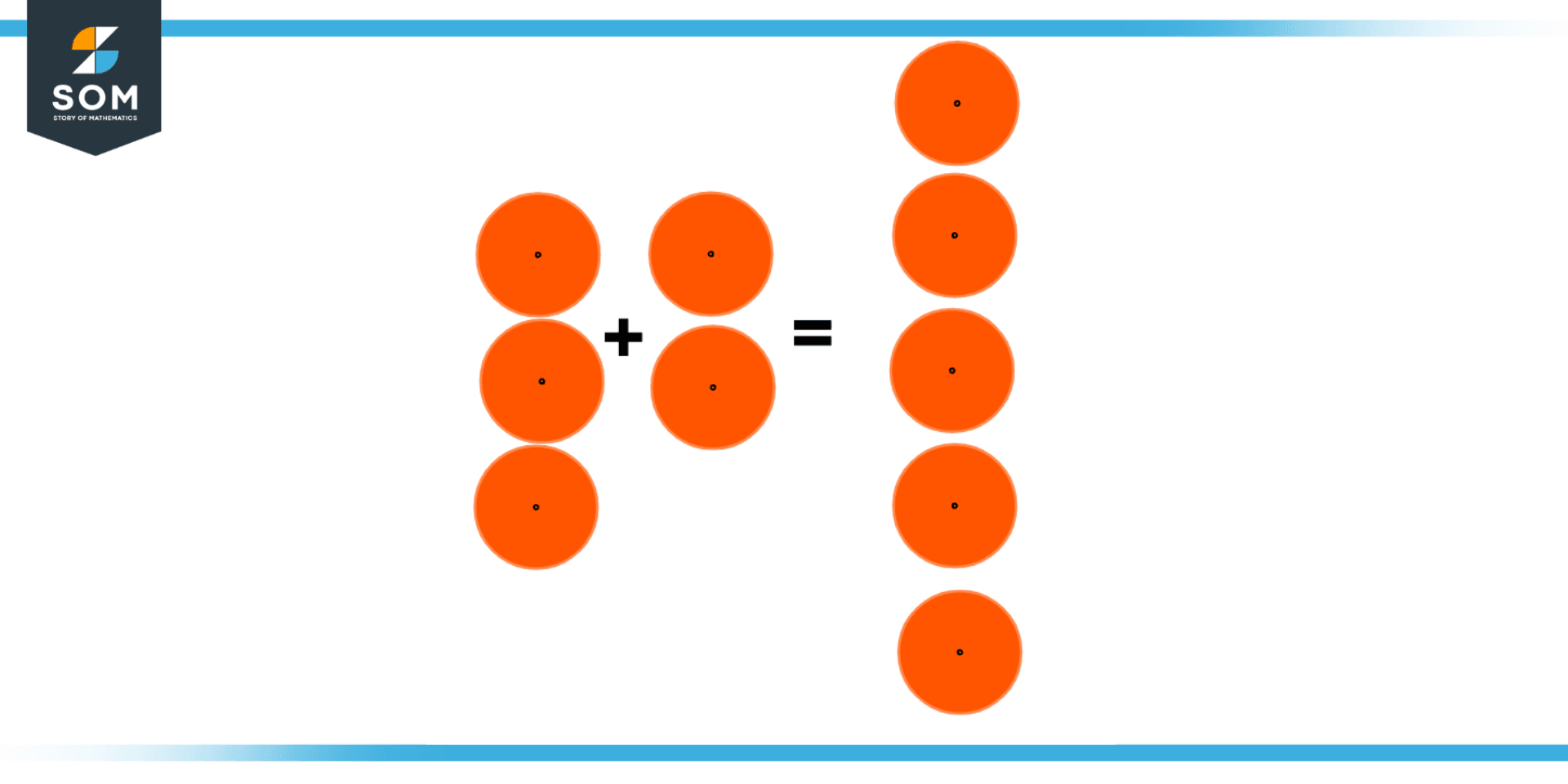
Figure 2 – Addition of Circles

Consider the above figure the first addend is 3 circles, and the second addend is 2 circles when the addition operation is applied, it results in 5 circles as shown

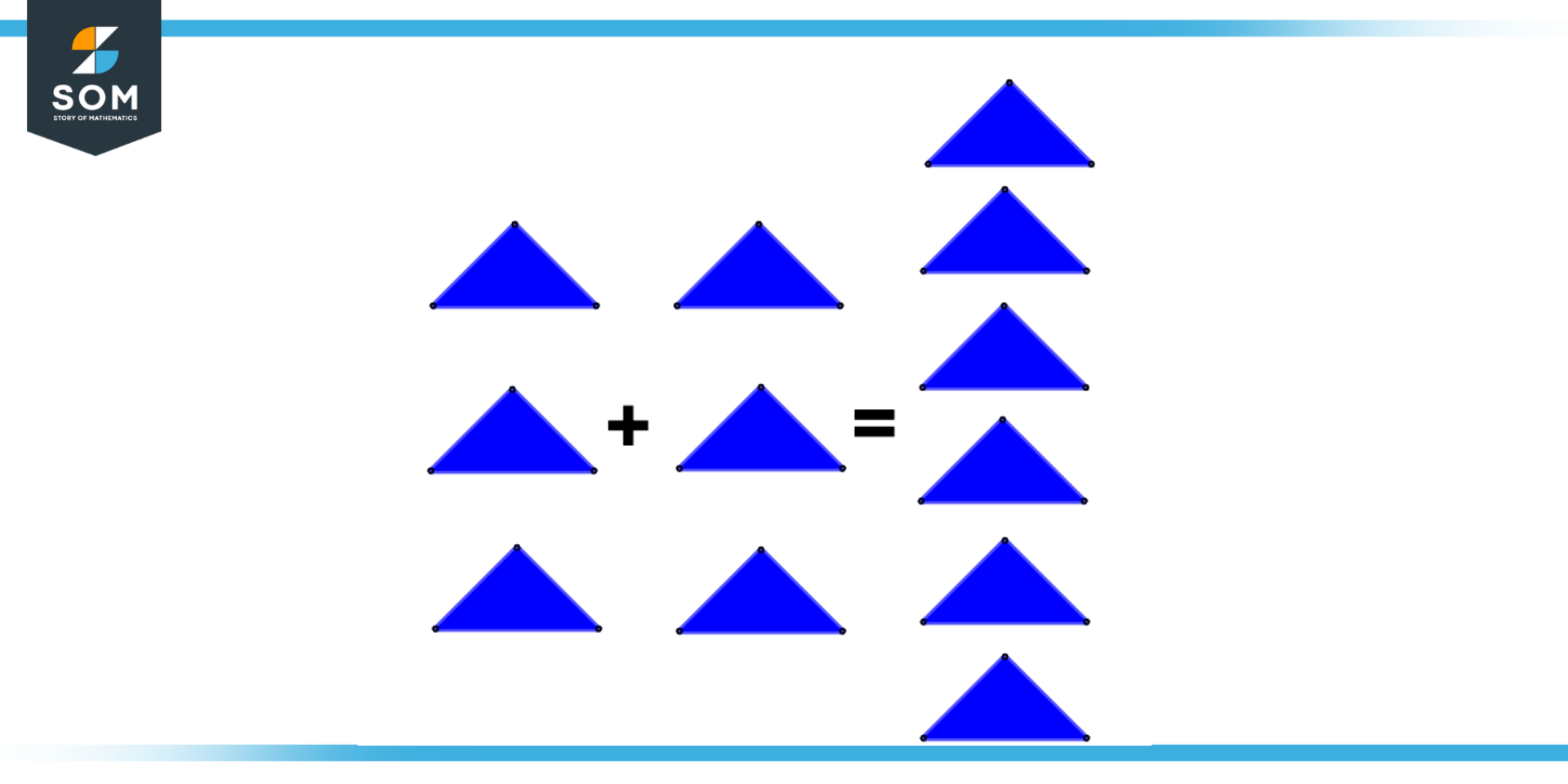
Figure 3 – Summing Triangles

Consider the above figure. The first addend is 3 triangles, and the second addend is 3 triangles, when the addition operation is applied it results in a sum of 6 triangles. 

Structure of Addition

The addition structure can be broken down as follows

Addend

The desired terms or numbers that are required to be added are known as an addend.

Sum

The result of addition or the result after applying the addition operator between the addend is known as the sum.

Symbol

Two lines are drawn horizontally and vertically to represent the addition symbol. Additionally, it has been referred to as the plus sign (+).

Mathematical Representation

Addend + Addend = Sum

An Additional symbol (+) is placed between the addend and equal to symbol (=) is placed before the sum.

Properties of Addition

There are three main properties of addition are:

• Commutative Property

It states that changing the order of addend does not affect the sum or result of addition for example: if there are two addends let’s say x and y and we apply the addition operation on it then the following equation holds which shows the commutative property of addition.

X + Y = Y + X

Verify

Let X=4, Y=2

4+2=2+4

5=5

This shows that addition holds the commutative property.

• Additive Identity Property

It states that when zero (additive identity) is added to any other addend the result or sum which we get will be equal to the addend to which we have added zero in other words adding zero to the addend gives the addend itself. Consider the following equation:

 0 + X = X

Verify

Let X=8

0 + 8 = 8

Which shows that addition holds additive identity property.

• Associative Property

It states that a sum of at least three or more than three addends results in the same sum irrespective of the fact that how these addends are grouped in other words we can say the grouping of addends is independent of the sum. Consider the following equation:

X + (Y + Z) = (X+ Y) + Z

Verify

Let X=9, Y=5, Z=3

9 +(5+3) = (9+5) +3

17=17

Which shows that addition holds the associative property.

Brief Description

While countering problems of addition, the addition operator can be applied easily on single-digit numbers, but for numbers greater than single-digit numbers, we have to break the numbers like units, tens, hundreds, and so on. As per the place value system, we always start adding from the right-hand side. Starting with one (units), we move to tens, then hundreds, and then so on. There may be carry in some cases while we are solving such problems and there may be none.

Let’s take different examples to understand the concept of addition.

Suppose there are three students, the first student has 5 apples, the second student has 3 apples, and the third student has 9 apples, and we are required to apply the concept of addition to this scenario then we will take these apples simply as addends 5, 3 and 9 and apply the addition operator as 5+3+9 that will give the sum equal to 17.

Let’s take another example: suppose we go to a grocery store, and we buy 5 bottles of juice and 1 bottle of milk. 5 packets of biscuits and we want to know the total quantity of items we purchased so we will add all the items as

          5 (bottles of juice) + 1 (bottle of milk), + 5 (packets of biscuits) = 11 items

Suppose you have 10 dresses and your friend gifted you 2 dresses then the total dresses you have will be equal to 12 dresses after applying the addition operation.

A Few Examples of Addition

Example 1

Consider there are two classrooms, students present in the first classroom are 20, and students present in the second classroom are 30. Find the number of students present in both classes.

Solution

First, convert descriptive data into a compact form.

Students in the first classroom=20

Students in the second classroom=30

The total number of students in both classrooms=?

Total number of students in both classrooms = Students in the first classroom + Students in the second classroom

Total number of students in both classroom = 20 + 30

Total number of students in both classrooms = 50

Example 2

Your mom went to a vegetable shop, and she bought 2kg of onions, 3kg of tomatoes, and 1kg of carrots. Find the total weight of the vegetables your mom bought.

Solution

Weight of onions= 2kg

Weight of tomatoes=3kg

Weight of carrots =1kg

Total weight = Weight of onions + Weight of tomatoes Weight of carrots

Total weight =2kg + 3kg + 1kg

Total weight=6kg

Example 3

Messi read 30 pages of a book in 50 minutes on Monday, the next day (Tuesday) he read 25 pages of books in 90 minutes, and on Wednesday he read 13 pages of a book in 30 minutes. How many pages of books did he read in three days? and how much time did he read in three days?

Solution

Pages read on Monday=30

Pages read on Tuesday=25

Pages read on Wednesday=13

Total pages read in three days= 30+25+13=68

Time spent on reading on Monday=50

Time spent on reading on Tuesday=90

Time spent on reading on Wednesday=30

Total time spent on reading in three days= 50 + 90 +30=170

Example 4

Apply the addition operator on two numbers 150,30 and show the results.

Solution

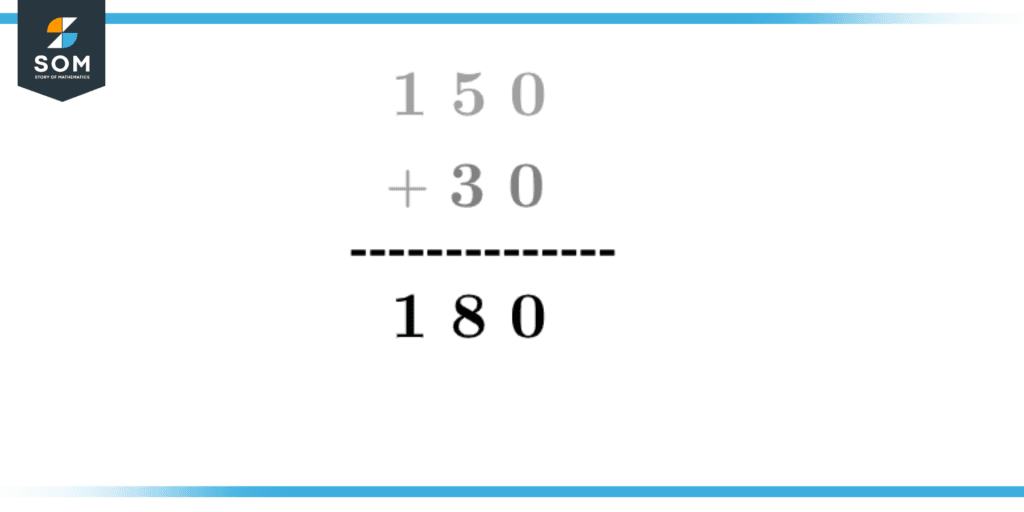
Figure 4 – Addition of Numbers

All mathematical drawings and images were created with GeoGebra.

Addend Definition < Glossary Index > Additive Identity Definition