JUMP TO TOPIC
Additive Identity|Definition & Meaning
Definition
The additive identity of a given number n is an element x, such that: n + x = n = x + n, where the number n belongs to an N set of numbers. N can be any number system. N can be a system of integers, rational numbers, real numbers, or complex numbers. N can also be replaced with matrices, vectors, or sets.
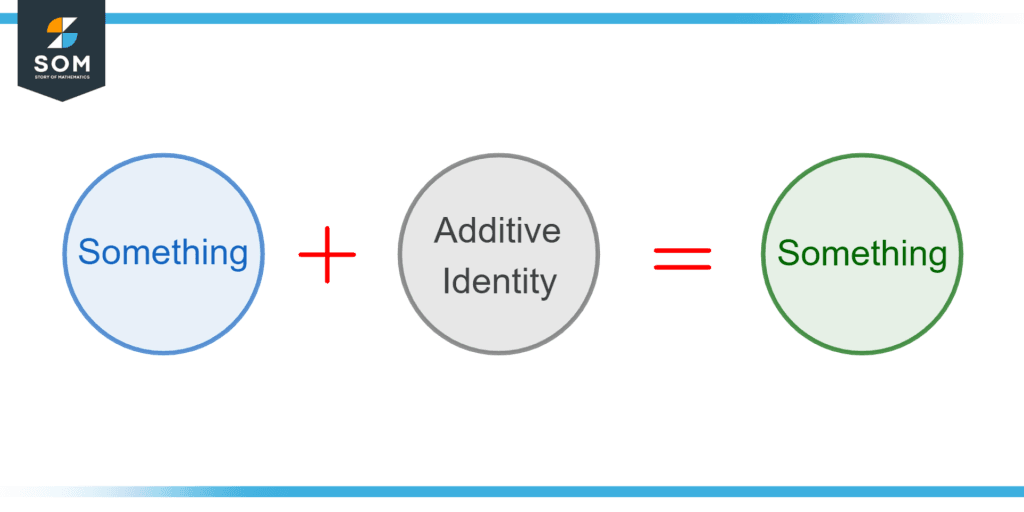
Figure 1 – The notion of additive identity in mathematics.
An additive identity is a property of a number system such that it yields back the same number when added to any number belonging to that specific number system. This number, usually referred to as an entity, term, or identity element, is mostly 0. This concept can be extended into sets, matrices, and vectors.
Representation of Additive Identity in Number Systems
As mentioned earlier, the concept of an additive identity can be represented in all number systems as its understanding is universal for all of them. The representation can be slightly different for each.
Following are some ways in which it is shown:
- Real numbers: 0 + a = a = a + 0, where a is any real number.
- Complex number: 0 + ai = ai = ai + 0, where ai is a complex number.
- Integers: 0 + n = n = n + 0, where n can a positive or negative integer.
In other representation media:
Vectors: 0→ + V→ = V→ = V→ + 0→, where the → sign represents vectors.
For natural numbers, being a subset of zero also means their additive identity is zero, as illustrated in the following figure:
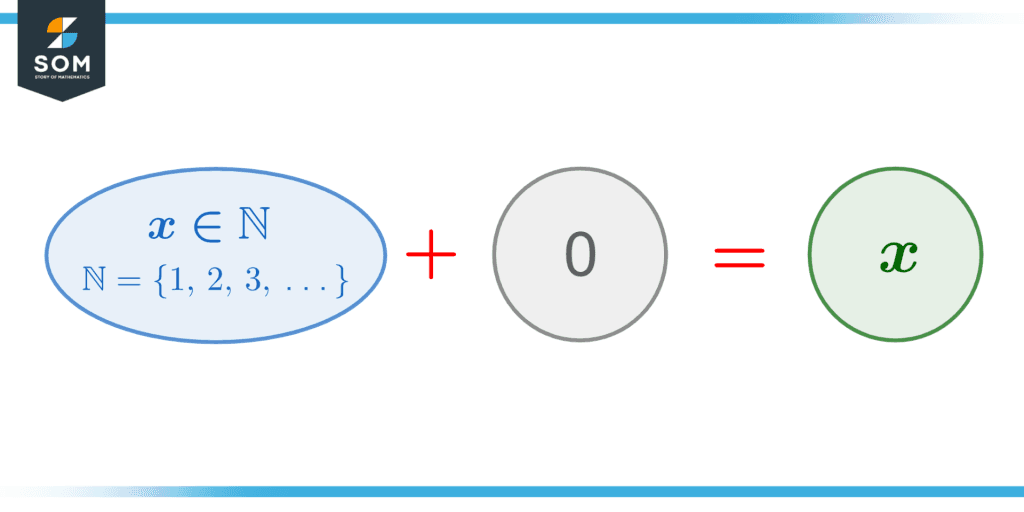
Figure 2 – Additive identity of natural numbers is 0.
Identity Element in Mathematics
Additive identity in mathematics is usually zero. It can be mathematically proven that any number when added to zero regardless of which direction you add it from, will always give you back the same number. This property is similar to all number systems having a slightly different representation in each. It is always true for the following relation:
e + n = n = n + e
where n is a part of the number system N.
The additive identity is a relatively easy concept to wrap one’s head around because of its simplicity. It is the simplest representation of the additive property.
It can be used as one of the basic criteria to judge whether a number belongs to a certain number system. For example, you want to find out whether the number -2 belongs to a group of integers. You can have multiple methods to test this but the most straightforward method would be to simply check it through this property. You can perform the following test:
0 + (-2) = -2 = (-2) + 0
The answer would be the same no matter where you approach the method from. This gives us one of, if not all, the indicators to categorize -2 as an integer.
As discussed, you can also extend this simple concept to other mathematical representations. For example, with matrices, you have a type of matrix called the null matrix. It is a matrix in which all the entries are zeroes. If you add such a matrix to any matrix with non-zero entries of the same order as the null matrix, the answer would be the matrix with the non-zero entries.
Another example of the usage of additive identity is in the form of sets. For example, you can have a null set (a set with no elements). You can add the null set to any set of numbers, like the set of whole numbers. When you add this null set to the set of whole numbers, the resulting answer would be the set of whole numbers.
Illustration of Identity Through Matrices and Sets
A null matrix is a matrix that has zeroes as all entries:
\[ O = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \]
The null matrix can be used as an additive identity to show the relation O + N = N = N + O. Where O is the null matrix and N is a matrix of the same order with non-zero entries.
Consider the non-zero matrix N:
\[ N = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \]
Then, the relations O + N = N and N + O = N, where O is the null matrix and N is the non-zero matrix.
\[ \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} + \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \]
\[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \]
Thus, if a number is added to an identity element, the result remains the same. Such a method can also be verified for vectors and sets.
When this null vector is added to a non-zero vector, it will reproduce the non-zero vector. For the sake of an illustration, consider the following non-zero vector A.
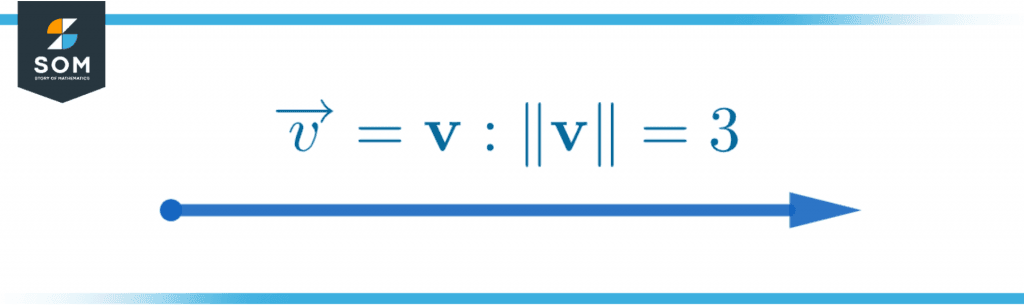
Figure 3 – A vector v with a magnitude of three.
A null vector is a vector with zero magnitudes and no direction. Consider the following null vector O.

Figure 4 – A null vector with zero magnitude and arbitrary direction as indicated by the lack of an arrowhead.
Now, if we add the vectors, they will give back Vector A in the resolution. It can be seen in the figure.
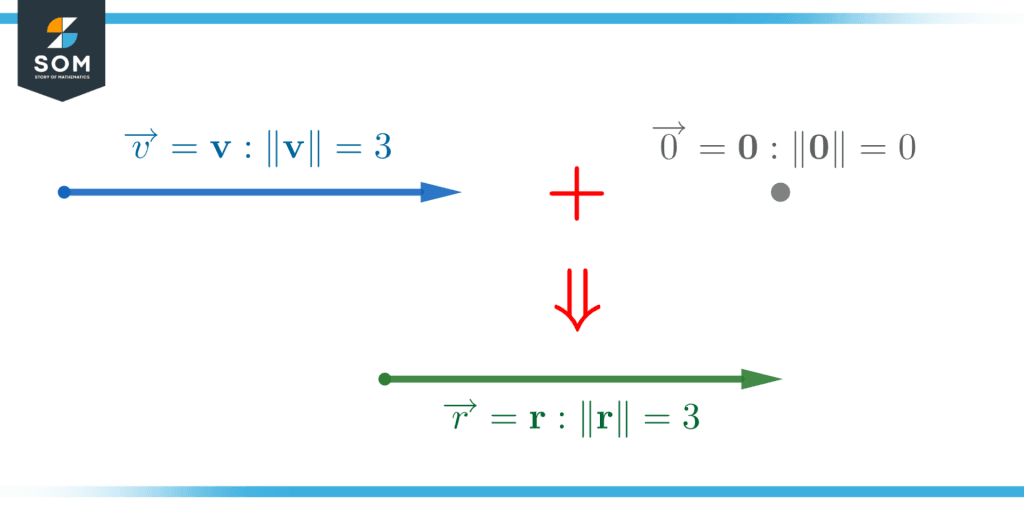
Figure 5 – Addition of vector v with the null vector. the result is the vector v.
Use of Additive Identity for Number System Verification
Use additive identity to verify whether the following numbers follow it or not:
1) 0 is the additive identity of -15
2) 0 is the additive identity of -4.5
3) 0 is the additive identity of 3i
Solution
1) 0 is the additive identity of -15
Let’s solve -15 (which is an integer) for additive identity, we apply the additive identity test to it. By following the definition n + x = n = x + n, we can solve it as follows:
(-15) + 0 = -15
0 + (-15) = -15
So, after performing the test, it is proven.
2) 0 is the additive identity of -4.5
We apply the additive identity test to it. By following the definition n + x = n = x + n, we can solve it as follows:
(-4.5) + 0 = -4.5
0 + (-4.5) = -4.5
So, after performing the test, it is proven.
3) 0 is the additive identity of the purely imaginary complex number 3i
We apply the additive identity test to it (0 + 0i). By following the definition n + x = n = x + n, we can solve it as follows:
3i + (0 + 0i) = 3i
(0 + 0i) + 3i = 3i
So, after performing the test, it is proven.
