JUMP TO TOPIC
Additive Inverse|Definition & Meaning
Definition
The additive inverse of a number can be defined as the numeral value, which will result in a zero value when added to the number. The two numbers are said to be additive inverses of each other if their addition results in a zero value.
Consider figure 1 for the additive inverse. If a number n is added with its additive inverse that will be -n, the result will be equal to zero. Similarly, the additive inverse of -n will be n.
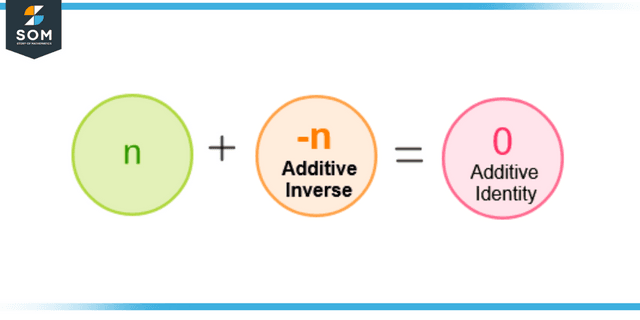
Figure 1 – Demonstration of Additive Inverse
Explanation of Additive Inverse
An additive Inverse is a value of any number that will give a zero result when added to any number.
If we add any two numbers and the result is zero, those two numbers are the additive inverses of each other. These two numbers can be in fractions, decimals, or imaginary numbers like iota.
Additive Inverse is the opposite value of a certain number or the negation of the number. This is because it has the opposite sign of the number whose additive inverse is required.
Use of Additive Inverse
The addition of the additive inverse of a number is typically used in equations to eliminate the number from one side of the algebraic equation.
Additive Inverse and Its Relation With Other Properties
The additive inverse is closely related to all the properties of real numbers when solving algebraic equations.
The additive identity is illustrated to understand the concept of the additive inverse. Both are closely related while dealing with the properties of real numbers.
In addition to this, multiplicative identity and multiplicative inverse are also demonstrated to compare the additive inverse with the multiplicative inverse.
Additive Inverse and Additive Identity
Additive Identity and additive inverse are related to each other as adding a number and its additive inverse always results in the additive identity.
They have a close relation and additive identity should be discussed to understand the additive inverse of a number.
Consider figure 2 for the additive identity. If a number m is added to the additive identity, then the result will be the same number m.
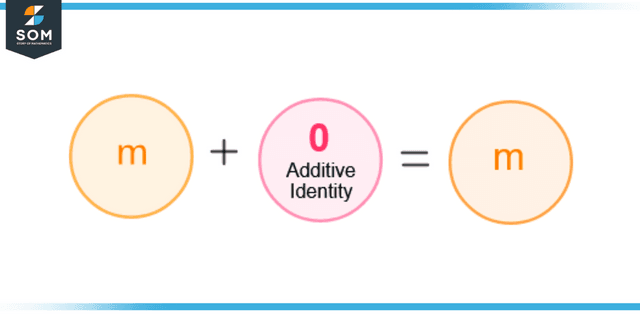
Figure 2 – Illustration of Additive Identity
Additive Inverse and Multiplicative Identity
Just like the additive identity, the multiplication of a number and its multiplicative inverse also results in the multiplicative identity.
Consider figure 3 for the multiplicative identity. If a number p is multiplied by the multiplicative identity, the result will be the identity of the number that is p.
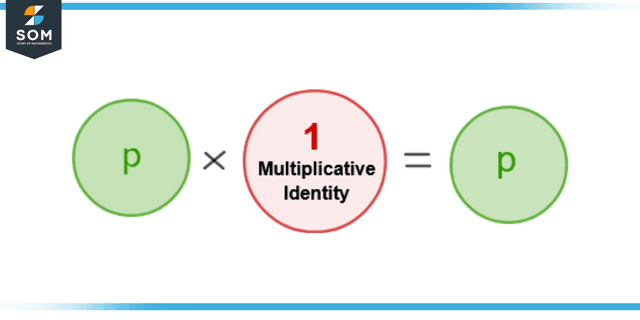
Figure 3 – Illustration of Multiplicative Identity
Additive Inverse and Multiplicative Inverse
In addition to this, the multiplicative inverse also has a close resemblance to additive identity. The additive inverse can be understood easily compared to a number’s multiplicative inverse.
Consider figure 4 in which the number s is multiplied by its multiplicative inverse to obtain the multiplicative identity that is one.
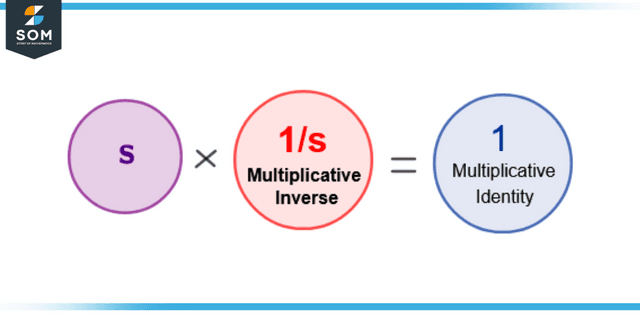
Figure 4 – Demonstration of Multiplicative Inverse
The multiplicative inverse of a number s is 1/s and of 1/s is s.
Explanations on Additive Identity, Multiplicative Identity and Multiplicative Inverse
The discussions on additive identity, multiplicative identity, and multiplicative inverse are made to have a thorough understanding of the additive inverse of a number.
Additive Identity
Additive Identity is a numerical value that when added to a number, the same number is obtained in the result.
As the name suggests, the additive identity gives back the identity of the number after the addition of the number with it.
The number that gives the same result when added to any given number is zero, so the additive identity is zero.
So, adding a number and its additive inverse will always result in the additive identity that is zero.
Multiplicative Identity
Multiplicative Identity is defined as the numerical value that when multiplied by a number gives the same number in return. It lets the number keep its identity even after the process of multiplication.
The concept of multiplicative identity is the same as additive identity with just the difference in processes that are addition and multiplication.
The multiplicative identity is one as it is the only number that is the same number after multiplying the number with it.
Just as the additive inverse, the multiplication of a number with its multiplicative inverse gives the multiplicative identity.
Multiplicative Inverse
The multiplicative inverse is defined as the numerical value that when multiplied by a given number gives the result as the multiplicative identity that is one.
Two numbers are considered multiplicative inverses of each other if their multiplication yields the result as one.
The multiplicative inverse of zero does not exist as the multiplication of any number with zero will always result in zero and never one.
Additive inverse and multiplicative inverses are used essentially when solving different algebraic equations.
Examples
Example 1
What are the additive inverse and the multiplicative inverse of -1/3? Check the result with the help of additive and multiplicative identities.
Solution
The additive inverse of -1/3 will be such a number that when added to it gives the result equal to zero which is the additive identity. So, the additive inverse of -1/3 is 1/3. The following solution checks the result for this answer.
Additive Inverse of -1/3 = 1/3
Check = -1/3 + 1/3 = 0
The multiplicative inverse of -1/3 will be -3 as the result of their multiplication will be equal to 1 which is the multiplicative identity. The solution for the multiplicative identity of -1/3 is given as follows:
Multiplicative Inverse of -1/3 = -3
Check = (-1/3) × (-3) = 1/3 × 3 = 1
Example 2
What are the additive inverse and the multiplicative inverse of 7? Also, provide the check for the answers.
Solution
The additive inverse of 7 is -7 as it is the same number but has the opposite sign.
It will also give the resultant as 0 if it is added to the given number which is 7. The answer can be checked by the following solution.
Additive Inverse of 7 = -7
Check = 7 + ( -7 ) = 7 – 7 = 0
For 7, the multiplicative inverse is 1/7 as the multiplication of the two numbers will give the result equal to 1. It can be confirmed by the solution as follows:
Multiplicative Inverse of 7 = 1/7
Check = 7 × (1/7) = 1
All the geometrical figures are created using GeoGebra.
