JUMP TO TOPIC
Adjacent|Definition & Meaning
Definition
The word “adjacent” is defined as lying next to or close to one another. It sometimes may not imply physical contact but certainly suggests that there is nothing in between the two entities of the same kind.
Figure 1 shows two balls lying adjacent to each other.
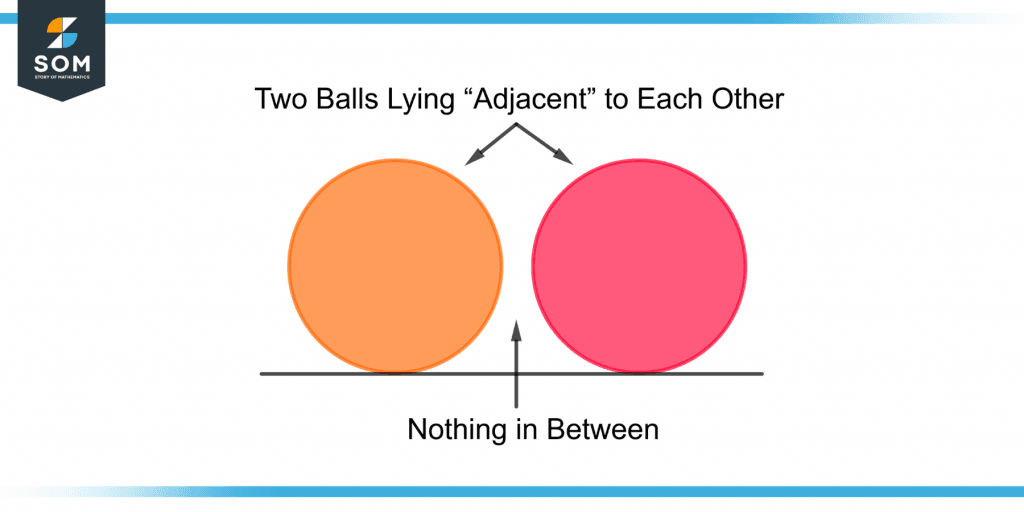
Figure 1 – Concept of “Adjacent” Demonstrated through Two Balls
Adjacent implies that the objects are placed in close vicinity. It does not suggest an overlap between the two objects meaning both objects have their separate physical space but are just attached through some means.
Explanation of Adjacent
Adjacent means neighboring to or adjoining to something. It is used as an adjective specifying the nearness of one entity to another.
For example, it can be used in a sentence as “The coffee shop is adjacent to the beauty parlor”.
In mathematical geometry, “adjacent” is used for the sides or angles which are joined by a common point, corner, or an end called a vertex. Vertices can also be adjacent to each other if they are adjoined by a line.
Adjacent Angles and Linear Pairs
Adjacent angles are important while dealing with linear pairs. Two adjacent angles are linear pairs if the sum of the adjacent angles equals 180°.
The two angles are supplementary with rays in the opposite direction not pointing to each other.
Non-Adjacency
Two angles are not adjacent if they are not opposed to each other from the common boundary line or side of the angle.
If the angles have a common side and vertex but are not facing opposite to each other but instead are overlapping, they are not considered adjacent angles.
Adjacent Sides, Angles, and Vertices
The word “adjacent” can be used for sides, angles, and vertices while dealing with geometrical shapes. The definitions for adjacent sides, adjacent angles, and adjacent vertices are as follows.
Adjacent Sides
Adjacent sides are defined as the sides which are connected by a point known as the vertex. One end of both sides is joined by a common corner which makes them adjacent to each other.
Adjacent sides can be found in geometrical shapes such as triangles, rectangles, parallelograms, or trapezoids involving line segments.
Adjacent Angles
An angle contains a vertex and two sides. Two angles having a common side and vertex are known as adjacent angles. In addition to this, both angles should not have common interior points.
Adjacency does not allow overlapping. The two adjacent angles cannot be overlapped over one another. This is the concept of the two angles not having the same interior points.
All three conditions should be met for the angles to be adjacent to each other.
Adjacent Vertices
A vertex is a point where two rays or two lines meet. Vertices can also be adjacent to each other. Two vertices are adjacent if they are joined directly by a line segment
In a square or rectangle, the corners are known as vertices. The pair of vertices joined by the sides of the square or rectangle are adjacent to each other.
Demonstration of Adjacent Sides, Angles, and Vertices
To understand the meaning of “adjacent”, consider the following illustrations for adjacent sides, adjacent angles, and adjacent vertices.
Consider figure 2 for the adjacent sides. The sides AB and BD are adjacent to each other as they are connected by a common vertex B. Similarly, the sides AC and CD, and BD and CD are also adjacent.
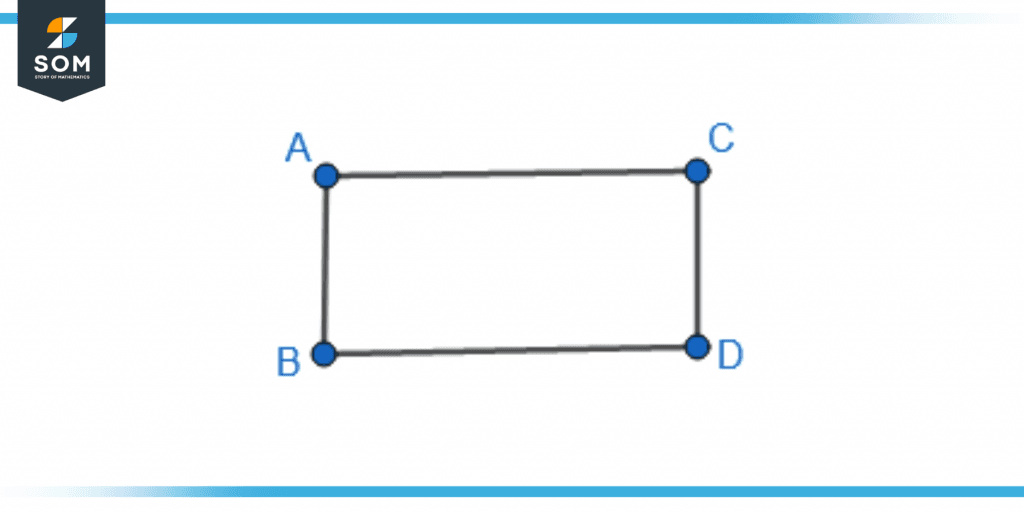
Figure 2 – Demonstration of Adjacent Sides in a Rectangle
But the sides AB and CD are not adjacent to each other as they do not share a common point.
Consider figure 3 for adjacent angles. The figure shows three angles; angle PSQ = a, angle QSR = b, and angle PSR = a + b. The angles PSQ and QSR are adjacent to each other as they share a common side QS.
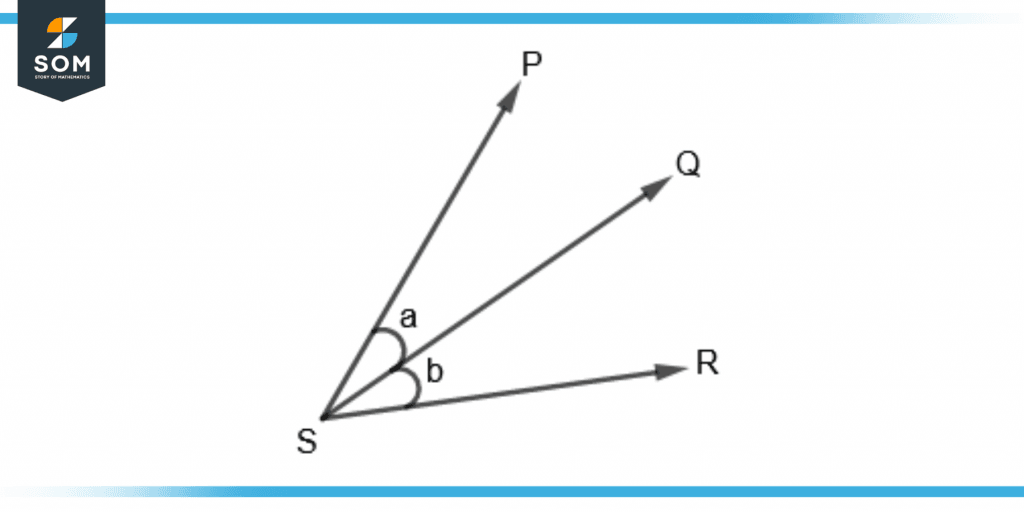
Figure 3 – Angles PSQ and QSR demonstrating Adjacent Angles
They also share a common vertex S and are not overlapping over one another thus one angle does not have interior points in the other angle.
The angles PSR and QSR have a common side that is SR and do have a common vertex S but are non-adjacent angles. This is because the angle QSR has interior points in angle PSR which shows an overlap between them.
Adjacent angles are opposite to each other. An angle bisector can make one angle into two adjacent angles.
Consider figure 4 for adjacent vertices. L, M, N, and O are vertices in the rectangle LMONL. Here f, g, h, and i are the edges or sides of the rectangle. The diagonal j can only be considered as an edge.
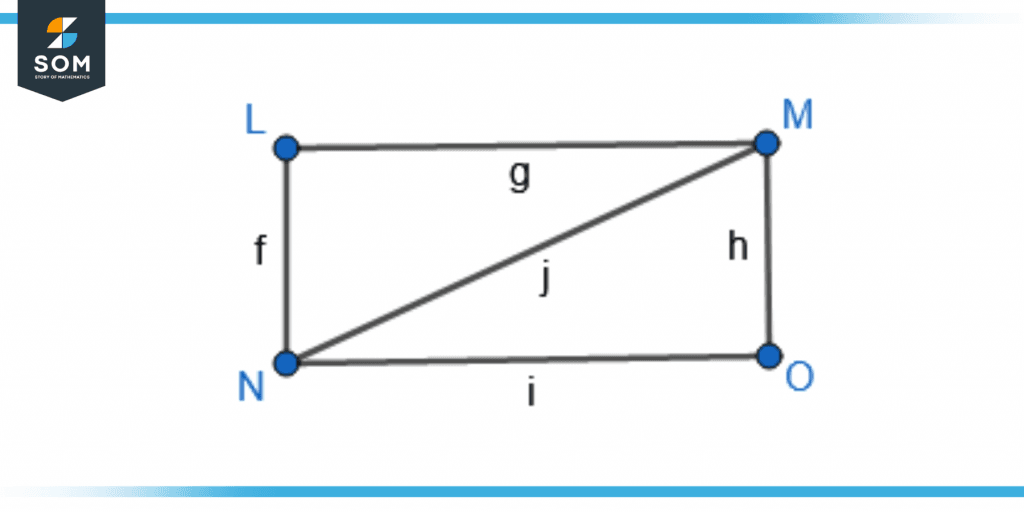
Figure 4 – A Rectangle showing Adjacent Vertices
The vertices L and M are adjacent to each other as they are directly joined by a side g. Similarly, the vertices N and M are also adjacent to each other as they contain an edge j joining them.
Adjacent vertices are also known as end-vertices. The vertices L and O are non-adjacent vertices as they are not connected directly by an edge.
Examples
Example 1 – Identifying Adjacent Sides
Figure 5 given below shows a triangle EFGE. Highlight the adjacent sides in the given triangle and explain what makes them adjacent.
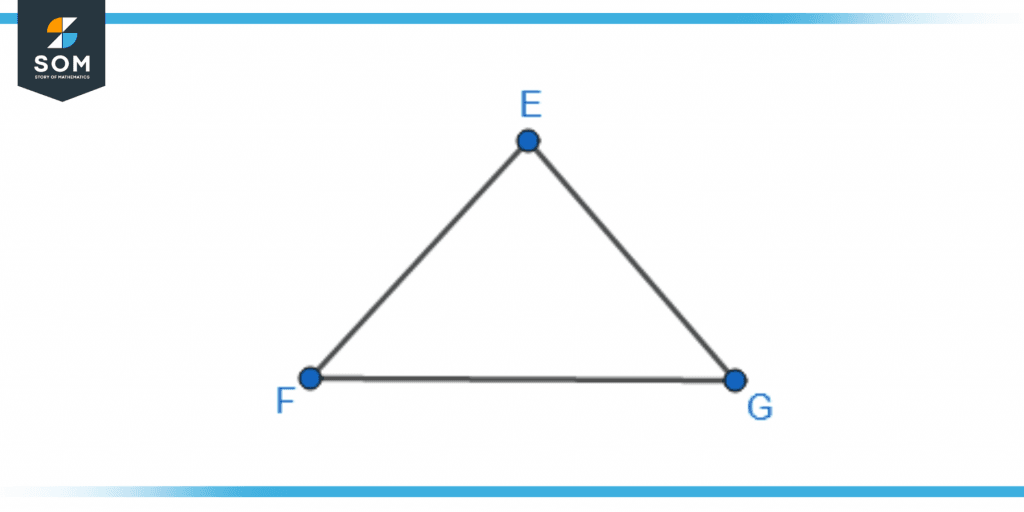
Figure 5 – Identifying Adjacent Sides in Triangle EFGE
Solution
The triangle contains the sides EF, FG, and GE. The sides EF and FG, FG and GE, and GE and EF are adjacent to each other. This is because they all contain a common corner or vertex F, G, and E respectively.
Example 2 – Identifying Adjacent Angles
The following figure 6 shows three angles; angle XWY = q, angle YWZ = p, and angle XWZ = q + p. Show which angles are adjacent and which are non-adjacent to each other.
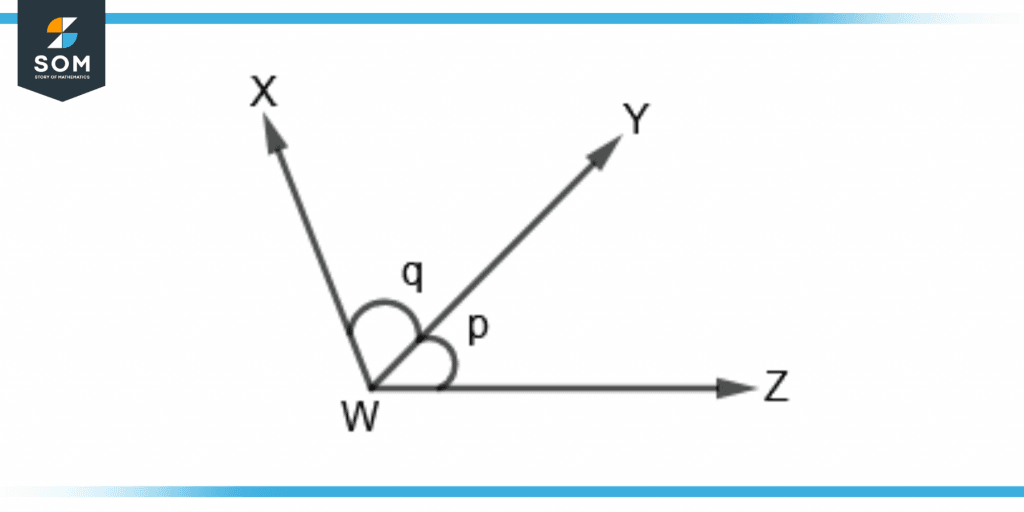
Figure 6 – Identifying Adjacent Angles
Solution
The angles XWY and YWZ are adjacent to each other as they share a common vertex W and a common side YW. They also are connected in opposite directions to each other.
Whereas, angles XWY and XWZ, and angles YWZ and XWZ are non-adjacent angles as they are overlapping with each other.
Example 3 – Identifying Adjacent Vertices
Figure 7 shows a square ABCDA. Point out the adjacent vertices and one non-adjacent vertex.
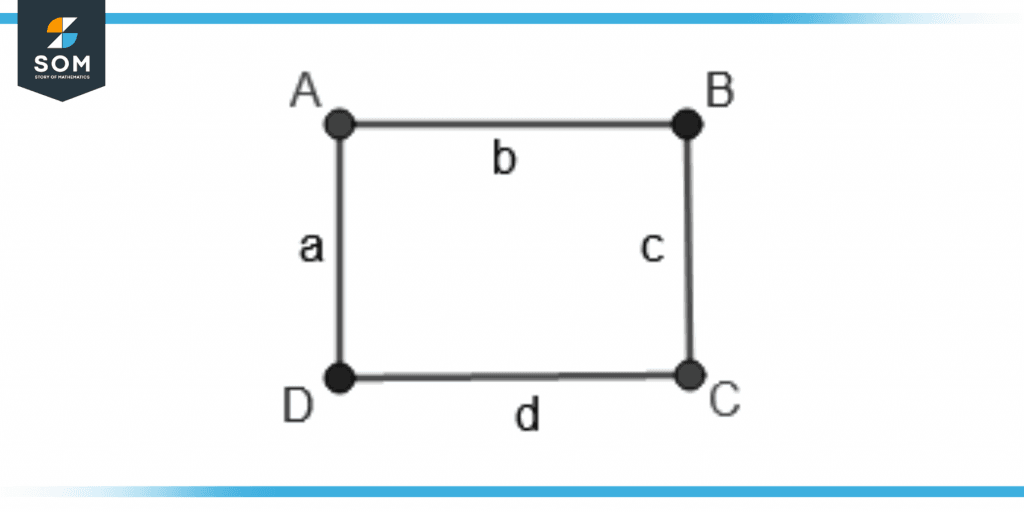
Figure 7 – Identifying Adjacent Vertices from Rectangle ABCDA
Solution
The vertex A and B, B and C, C and D, and D and A are adjacent vertices with b, c, d, and a as the edges or sides joining the vertices.
All the geometrical figures are created using GeoGebra.
