Adjacent Angles|Definition & Meaning

Attributes of Adjacent Angles

Adjacent angles are any two angles that have:

1. Same vertex
2. A common side
3. No overlapping between the angles

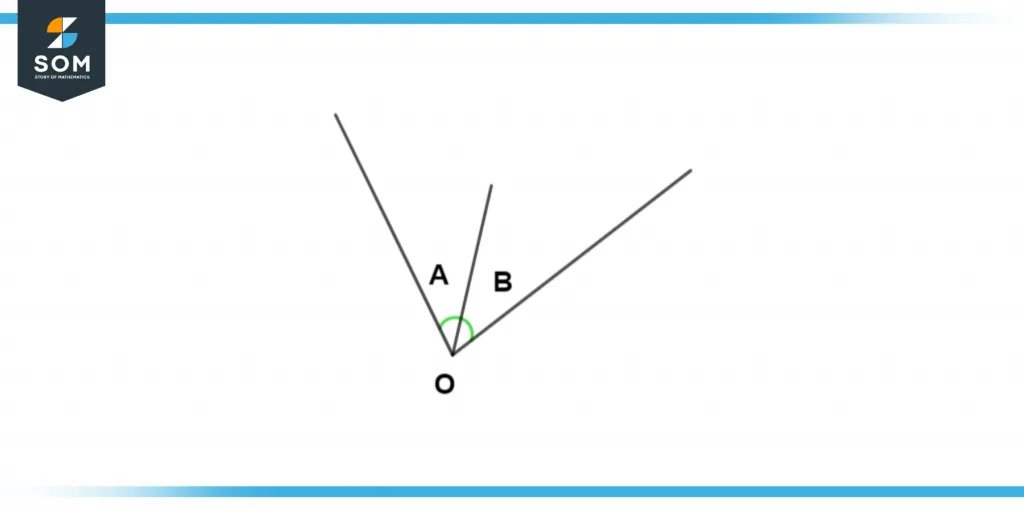
Figure 1 – Adjacent Angles

They will be considered as adjacent angles but if either one of these properties is not met then we won’t consider those angles as adjacent angles. We can further divide the adjacent angle into 2 parts; a complementary angle and a supplementary angle. 

Detailed Explanation Adjacent Angles

Let us consider 2 slices of pizza in a box. Both the slices have the same endpoint and share a common side. And they are not overlapping each other at all. Similarly, we can find numerous daily life examples.

Let us consider the following figure to help us understand the concept of adjacent angles

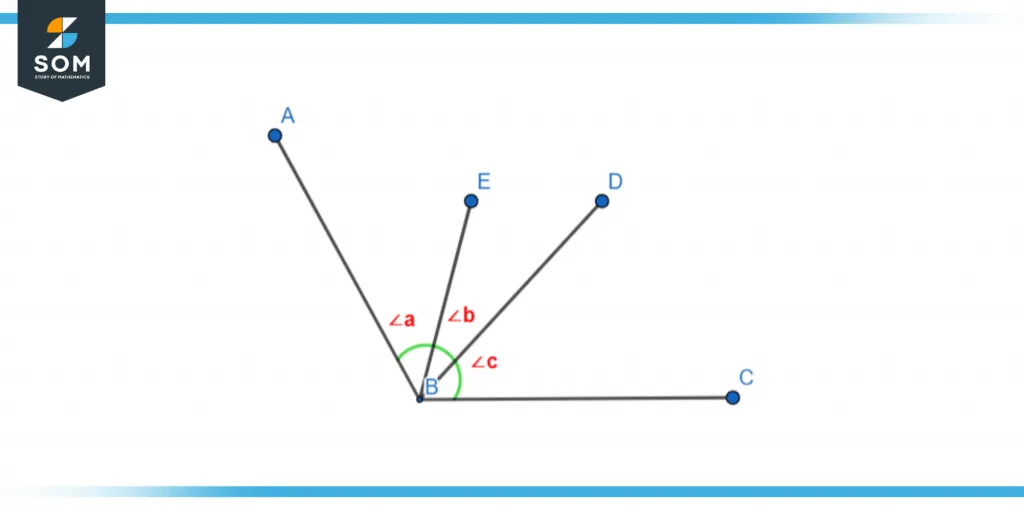
Figure 2 – ∠ABC

In this figure, we can see that ∠a and ∠b are adjacent to each other. They have a common vertex at point B and share a ray. But ∠a and ∠c are not adjacent to each other. This is because they do not share a common side and by definition, we know that all properties must be fulfilled for any 2 angles to be identified as adjacent angles.

We can use this concept to identify and differentiate between an adjacent angle and a vertical angle. Imagine a line intersects another line while forming a cross, such that we have 4 angles. As we know that adjacent angles will always have two properties; the same vertex and common side.

Similarly, we can identify a vertical angle which is a set of angles that have the same vertex but do not share a side. These angles may be opposite to each other which are known as vertically opposite angles.

Now let us use the same example of a line that intersects another line to form a cross to understand the concept of linear pair. Linear pairs are such adjacent angles whose sum is always equal to 180 degrees. The angles in a linear pair are always supplementary to each other.

Note that all linear pairs are supplementary but not all supplementary angles are linear pairs. This is because to form a linear pair we need an intersection between two lines and the presence of adjacent angles. If we have a linear pair and its angles add up to be equal to 180 degrees then its non-common arm will form a line.

Adjacent angles can be complementary angles to each other if the sum of the two angles equals 90 degrees. Similarly, if the sum of such angles is equal to 180 degrees they will be supplementary to each other.

Properties of Adjacent Angles

We know that every adjacent angle has certain following properties which make them stand out from other angles. The following properties help us identify adjacent angles:

1. All angles will share the same vertex
2. Adjacent angles share a common side or ray
3. They must not overlap with each other
4. Along with a common side, each angle should have an uncommon side of its own
5. The Sum of the adjacent angles define whether they are complementary or supplementary
6. The angles must not have a common interior point but should be separated
7. All adjacent angles exist in pairs

Additional Illustrations of Different Adjacent Angles

We will now understand the concepts of adjacent angles by using a pictorial format.

The example given below shows adjacent angles:

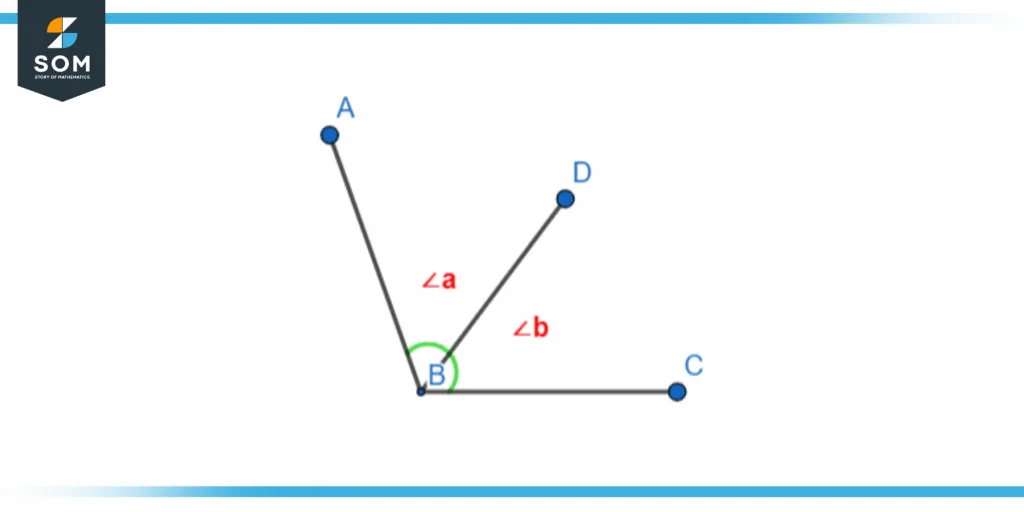
Figure 3 – Adjacent Angles

In this diagram, we can see that both angles ∠a and ∠b are adjacent to each other as they both share the same vertex at point B and both angles are using the line BD commonly.

Let us look at the following image:

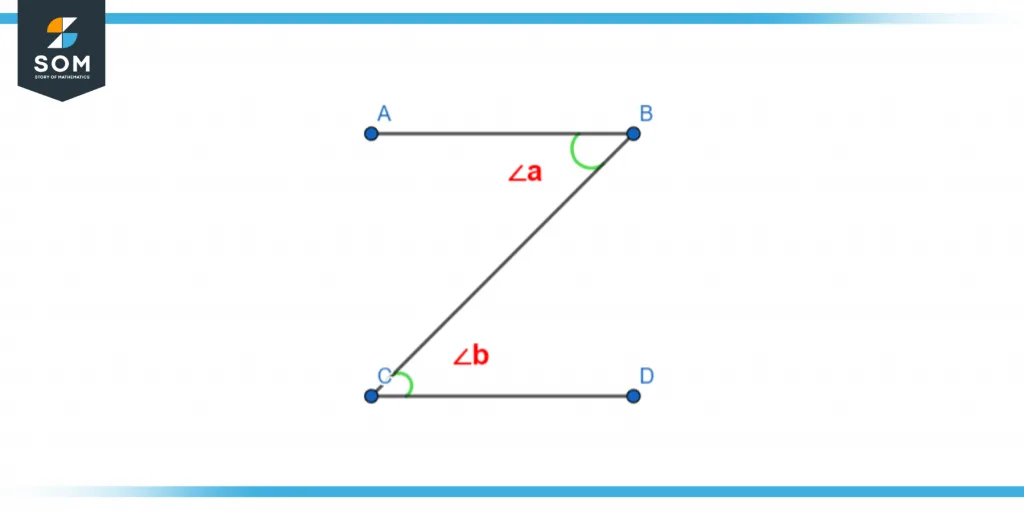
Figure 4 – Non-Adjacent Angles

In this figure, we can see that both angles ∠a and ∠b share a common side but they will not be considered adjacent angels because they don’t have the same vertex.

Now to understand the linear pair’s concept we will refer to the following figure:

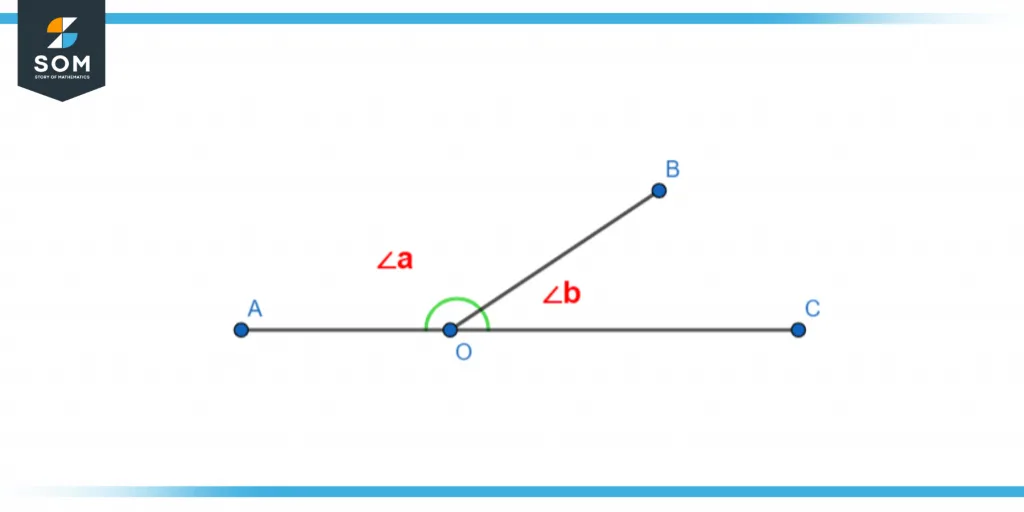
Figure 5 – Linear Pairs

As we can see that both angles ∠a and ∠b, when added together, are equal to 180 degrees which means that they are linear pairs and the uncommon sides have formed a straight line.

Solved Examples of Adjacent Angles

Example 1

Using the figure, find:

∠ZOY = ?

Where:

∠XOZ = 80°

∠XOY = 120°

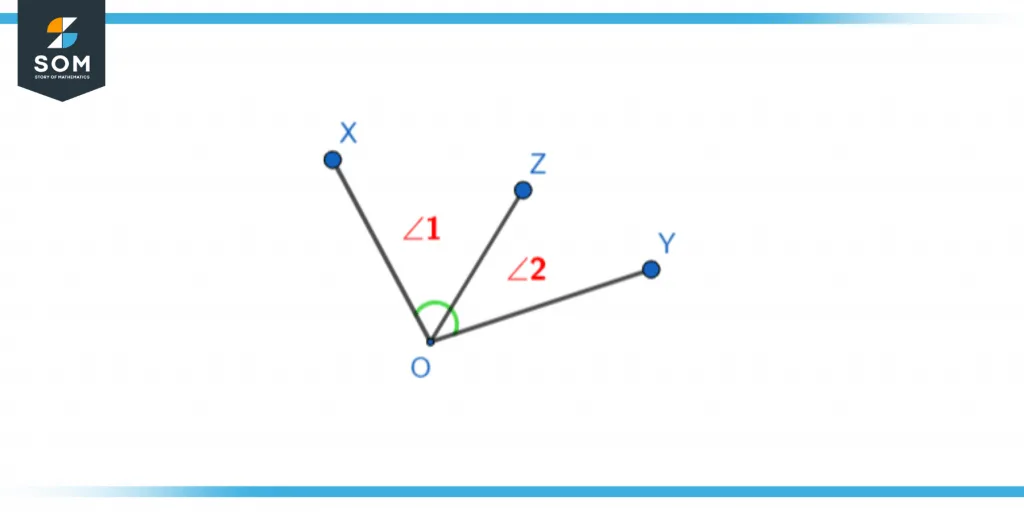
Figure 6 – ∠XOY

Solution

From the given figure:

m∠XOY = 120°

m∠ZOY = a

m∠ XOZ = 80°

By using this formula:

∠XOY = ∠ZOY + ∠XOZ

m∠XOY = m∠ZOY + m∠XOZ

120° = a + 80°

a = 120° – 80°

a = 40°

Hence the angle ∠ZOY is equal to 40°.

Example 2

Thomas has been assigned geometry homework in which he has to identify whether the following figure is of adjacent angles or not. Help him identify and explain with reasoning.

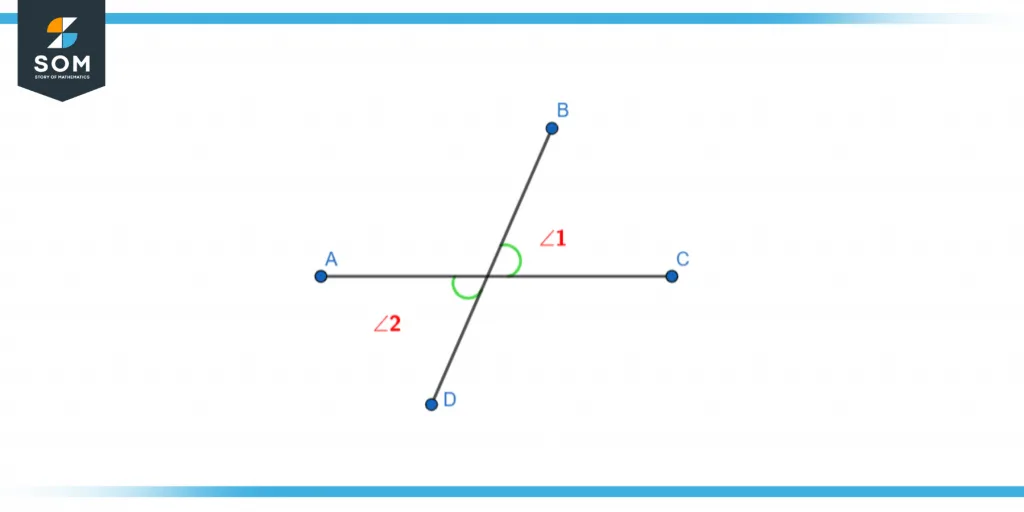
Figure 7 – ∠ABCD

Solution

The following figure does not satisfy the properties of adjacent angles as they are vertically opposite to each other.

They are equal in measure but opposite in direction so they are called vertically opposite angles or simply vertical angles.

Example 3

Miranda is teaching the basics of geometry to 4th graders. She wants to give them real-life examples corresponding to her topic which is ‘Adjacent Angles’. Help her deliver her lecture more effectively by providing real-life examples.

Solution

Some examples of adjacent angels that we see on the daily basis are:

1. The hands of the clock represent adjacent angles as they all have the same vertex and a common side. This example can only be used when all three hours, minutes, and seconds hand are away from each other and not overlapping.
2. Cake slices on a plate represent adjacent angles as they satisfy the properties.
3. Blades of a windmill form adjacent angles.
4. A ladder placed against the wall at a certain angle is an example of linear pair.
5. A T-junction road represents adjacent angles
6. A justice balance also represents adjacent angles

Images/mathematical drawings are created with GeoGebra.

Adjacent Definition < Glossary Index > Adjacent Side Triangle Definition