Adjacent Side (Triangle)|Definition & Meaning

What Is the Adjacent Side of a Triangle? 

The adjacent means next to so the side which is next to the given angle is the adjacent side. The side that is perpendicular to the right angle is always considered to be the hypotenuse. In a right triangle, this is the side that is the longest. The terms “opposite” and “adjacent” are used to refer to the two remaining sides. The names of these sides are derived from their relationships to certain angles. The side which is opposite to the hypotenuse is adjacent.

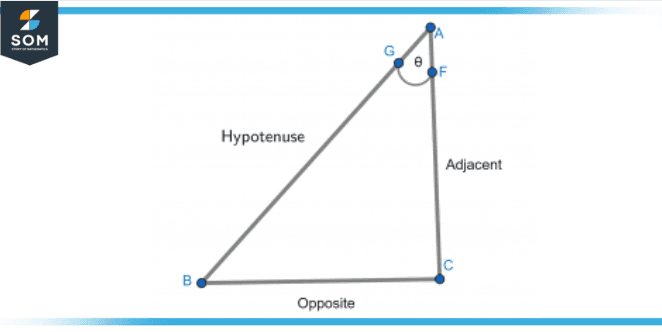
Figure 1 – The right angle triangle with the angle between adjacent and hypotenuse side

Detailed Explanation

Here in this article, you will find a detailed explanation of the sides of triangles mainly adjacent sides with examples for better understanding. The study of trigonometry and every other type of polygon can be broken down into triangles. Therefore, trigonometry emerges as an essential component of the overall subject of plane geometry. The understanding of the sides and angles of triangle is of great importance to analyzing different types of triangles.

Sides of Right Angle Triangle

There are three sides to the triangle

1. Adjacent
2. Hypotenuse
3. Opposite

The right triangle’s three sides’ relationship to one another is the subject of Pythagoras’ Theorem. According to Pythagoras‘ theorem, the hypotenuse square is equivalent to the sum of its other two sides. The triangle has three sides which are connected end to end with each other.

The hypotenuse is the side that is the longest in a right triangle. A side that is “opposite” is the side that is direct across from the given angle and that is the adjacent side. The hypotenuse, the opposite, and the adjacent are the three sides that a triangle has and the three angles that make a triangle.

The trigonometric functions have this as their foundation.

Cos(θ) = opposite/hypotenuse

Sin (θ) = adjacent/hypotenuse

Tan(θ) = adjacent/opposite

Csc(θ) = hypotenuse/adjacent

Sec(θ) = hypotenuse/opposite

Cot(θ) = opposite/adjacent

These are all the trigonometric functions in which the sides are considered. Without knowledge of the sides of a triangle, trigonometry will not be solved.

Visualizing Adjacent Sides in Triangles

For understanding trigonometric functions and geometry the sides and the angle concepts must be clear. A triangle with a right-angled is one that has three angles and three sides.

The right angle is the angle that is perpendicular to an adjacent side. The longest side of a right-angled triangle, which is the side that is opposite the right angle, is called the hypotenuse. The side in between the angle concerned and the right angle is referred to as the neighboring side or adjacent side. The angle in concern is opposite the opposite side or perpendicular.

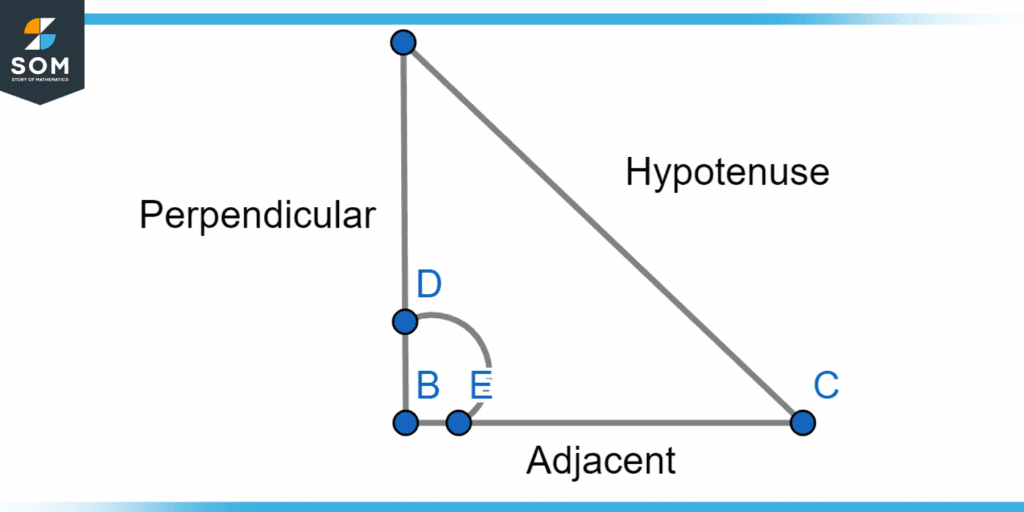
Figure 2 – Right Angle Triangle with the angle between the perpendicular and adjacent side.

In a right-angle triangle, the side which is facing the right angle is always hypotenuse however the remaining two sides are either adjacent or opposite. It depends on the relationship between the angle and the sides.

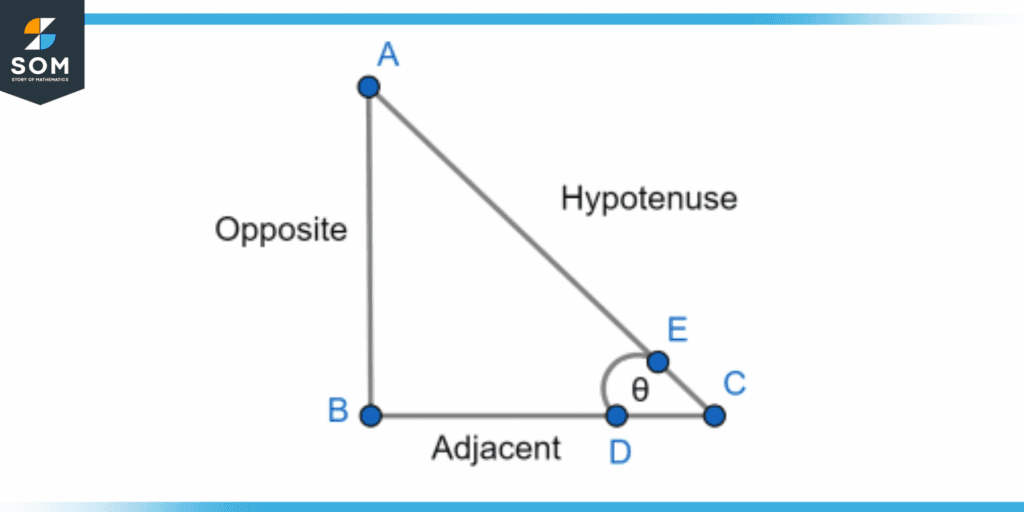
Figure 3 – Right angle triangle with the angle between hypotenuse and adjacent side

The figure above is the second type of triangle in this right-angle triangle there are three sides AB, BC, and CA. The angle θ is between sides BC and CA. The longest shown side is the hypotenuse which is side CA, opposite to the hypotenuse is the opposite side which is named AB and the adjacent side is the side that is exactly connected with the angle θ and the hypotenuse which is called side BC.

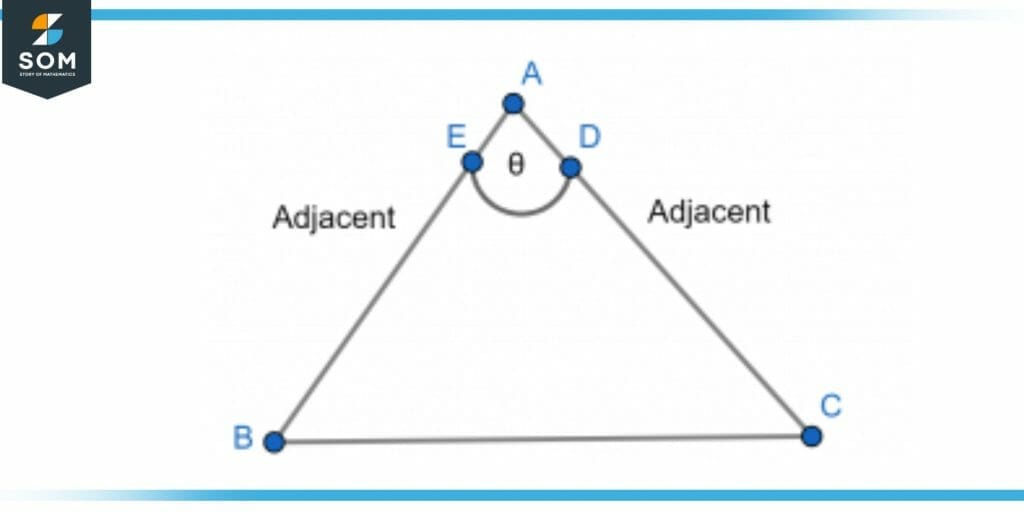
Figure 4 – A triangle with the angle between two adjacent sides

The above triangle is the third type of triangle. The triangle is measured as ABC, there are three sides named as AB, BC, and CA. The angle is present between side AB and AC. In another way the angle is in between two sides one is the longest side which is always hypotenuse and the other with the angle must be adjacent. The angle in this triangle is between two adjacent sides.

Here is another type of triangle which is a bit different than the above-explained triangles. In the above triangle, there are the same three sides but non of them is at the right angle. The triangle is named ABC the angle is with side AB and AD so the adjacent side is exactly with the angle shown, as this is not a right triangle so instead of hypotenuse there will be two adjacent sides. Above is a detailed explanation of three different angles’ positions so the sides will also be different, the name of the sides depends upon the position of a given angle.

Example

Here is an example of the sides of a triangle which will help in understanding further the terminologies and the concepts of the sides as well as angles of a triangle. Identify the side that is adjacent to the ∠θ, the side opposite to ∠θ, and the hypotenuse of the right triangle △ABC in the given diagram.

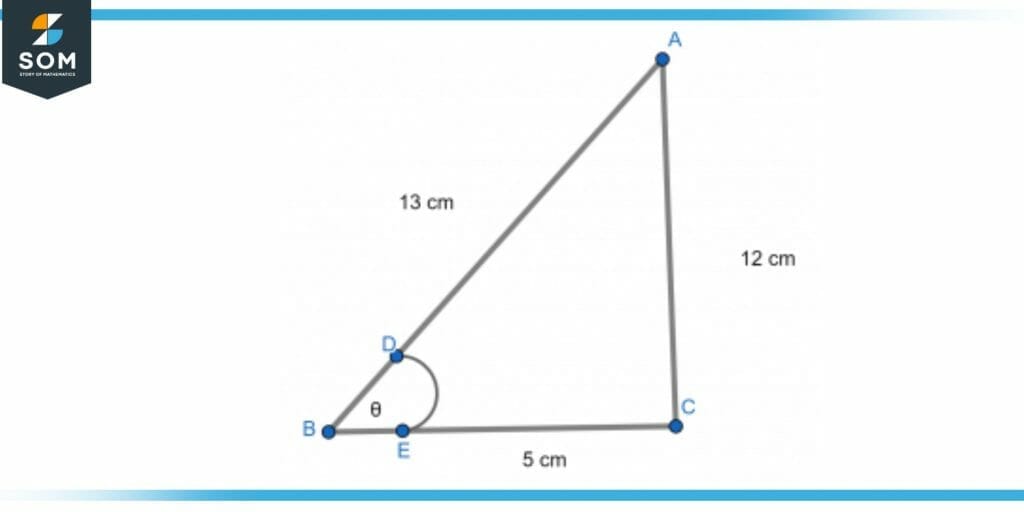
Figure 5 – Right angle triangle with sides ABC and angle in between adjacent and hypotenuse

Solution

The length of side AB which is hypotenuse is 13cm, and the length of the opposite side which is measured as AC is 12 cm whereas the length of the adjacent side which is with the angle is 5cm. Now, step-by-step explanations of the sides of triangle are explained below for better analysis.

Step 1: Have a look at the right angle triangle and identify the right angle, the side BC and AC are making an angle of 90°  with each other as they are perpendicular to each other so this angle is the right angle on the side opposite to right angle is the hypotenuse.

Thus AB is hypotenuse.

Step 2: Determine the angle to the respect of which the opposing are requested. The opposing side will be the side that is perpendicular to that angle.

The side opposite of ∠B is AC which is the opposite side.

Step 3: Find the side, other than the hypotenuse, that side is adjacent to that given angle. That side will be to the side.

Thus DE is the adjacent side of this triangle.

Images/mathematical drawings are created with GeoGebra.

Adjacent Angles Definition < Glossary Index > Adjacent Sides Definition