Adjacent Sides|Definition & Meaning

An adjacent side meets another side of the shape at some point. Adjacent means “side-by-side or adjoining,” and the vertex is the point at which two lines (or sides) join together. Therefore, when two sides share a vertex, they are adjacent. 

It is possible in some complex shapes for a side to be adjacent to more than just one other side (if three or more sides join together at the same vertex).

Understanding Adjacency Visually

Consider a triangle with vertices A, B, and C, as shown in the figure below.

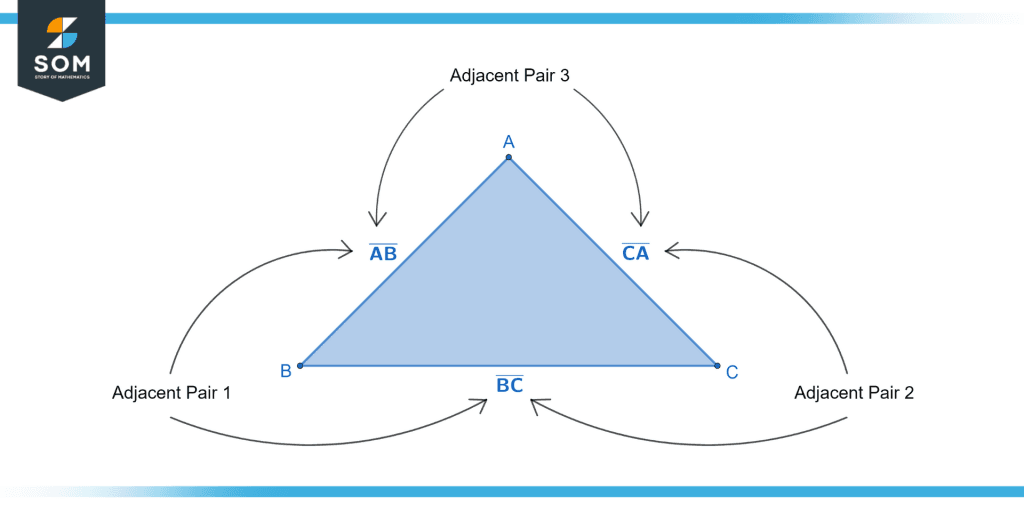
Figure 1 – Three pairs of adjacent sides in a triangle.

The three sides of this triangle are AB, BC, and CA. Since sides AB and BC share the common vertex B, they are adjacent. Similarly, sides BC and CA share vertex C, and sides CA and AB share vertex A. Thus, there are always three pairs of adjacent sides in a triangle.

Now let us look at a pentagon (see Figure 2) with five vertices A, B, C, D, and E. Here, you have the sides AB, BC, CD, DE, and EA. 

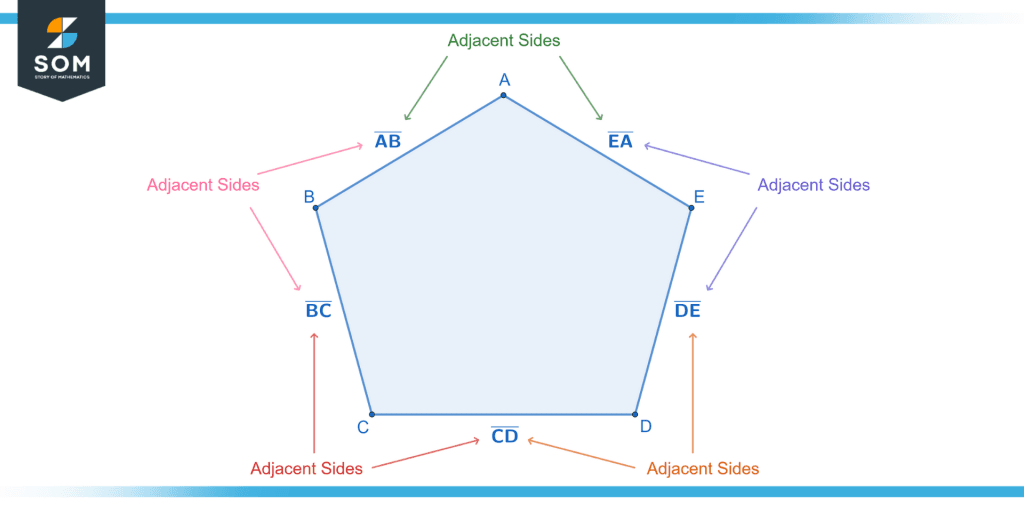
Figure 2 – Five pairs of adjacent sides in a pentagon.

We can see that side AB is adjacent to sides BC (common vertex B) and EA (common vertex A). Similarly, we can see that side BC is next to CD, side CD is next to DE, and side DE is next to EA. They respectively share the vertices C, D, and E. Therefore, we have five pairs of adjacent sides here.

Why Is Adjacency Important?

Adjacency is one of the critical visual cues for our brain to process the structured “oneness” of the shapes in our daily life. Like adjacent sides, we also have adjacent vertices and angles. These properties simplify geometrical shapes and allow us to analyze them properly.

For example, suppose you have three matchsticks arranged in the shape of a triangle. Now, imagine that you start taking the matchsticks far away from each other.

Eventually, the gap will be so large that it would be hard to think the matchsticks form a triangle! In this way, adjacency affects our perception of shapes.

Adjacent Sides in 3D

The method of determining adjacent sides in 3D remains the same: identify the lines that share a common vertex – they are adjacent. A 3D shape occupies space (three dimensions: length, width, and depth).

Usually, adjacency in 3D is associated with the shape’s faces. Nonetheless, adjacent sides are equally valid. 

For example, a cube has six faces (front, back, left, right, top, bottom). On its own, each face is a square. A square has four vertices, so each face has four pairs of adjacent sides. 

Now consider one side on a single face of the cube. Since a side has two vertices, and each vertex connects up to three sides (including the side we are looking at) in a cube, each side is adjacent to four other sides! You can verify this from Figure 4 in Example 2.

Opposite Sides

The opposite side of any given side is the one farthest away from it in the opposite direction. This is in contrast to adjacent sides. However, depending on the shape, a side can be opposite to another side or a vertex.

For example, if a polygon has an even number of sides, each side has an opposite side. On the other hand, if it has an odd number of sides, each side only has an opposite vertex.

Examples of Finding Adjacent Sides

Example 1

Find the total number of adjacent sides in a square with the diagonals drawn in and mention their shared vertices. 

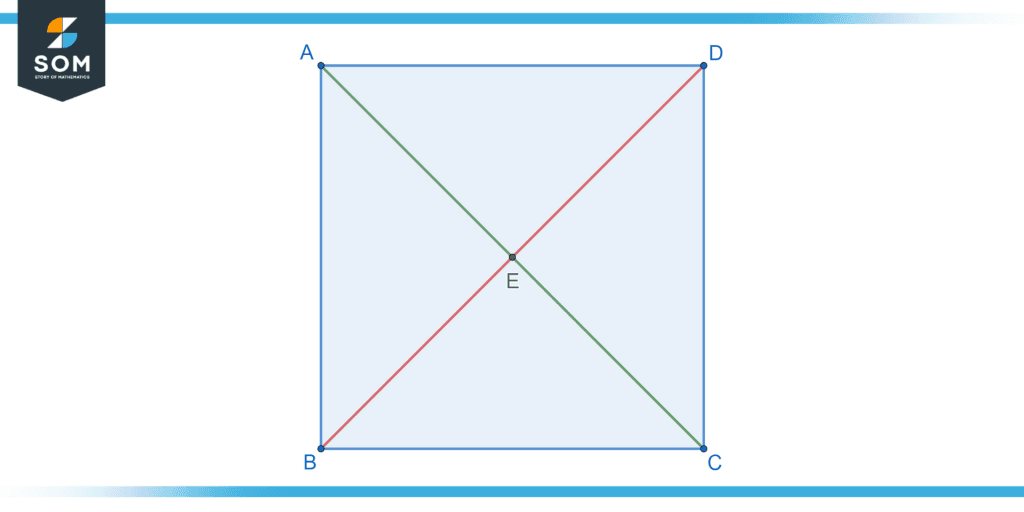
Figure 3 – Square with diagonals drawn in.

Solution

With the diagonals drawn in, we now have eight sides: AB, BC, CD, DA, AE, CE, BE, and DE. The common vertices joining the adjacent sides are:

1. A joins AB, AE, and DA
2. B joins AB, BE, and BC
3. C joins BC, CE, and CD 
4. D joins CD, DE, and DA
5. E joins AE, BE, CE, and DE.

Thus, each vertex has three adjacent sides, except for E, which has four. Adding them up, there are 2 x 4 + 6 = 14 pairs of adjacent sides in total.

Example 2

Brian is trying to figure out which sides of his friend’s 3-by-3 Rubik’s cube are adjacent. Extending the concept of adjacent sides to adjacent faces in 3D, try to solve the problem.

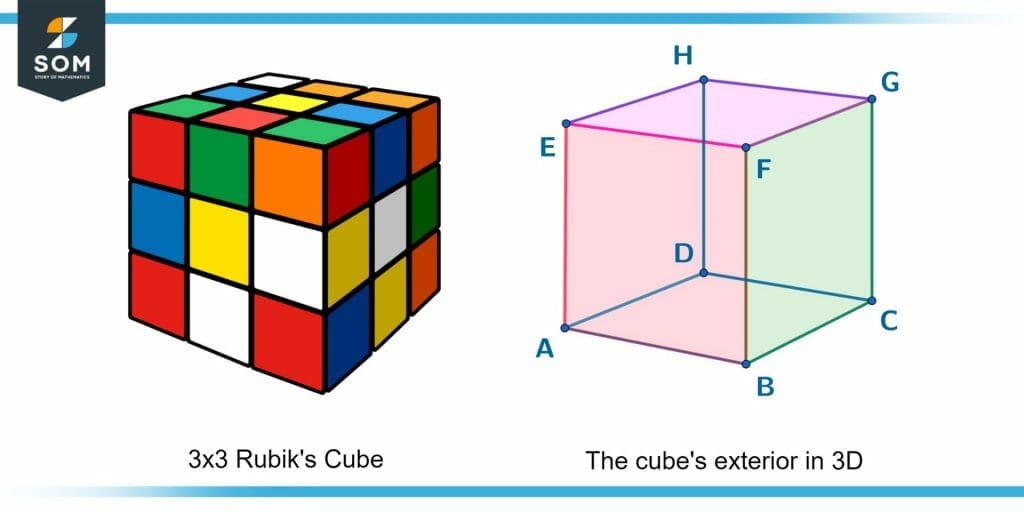
Figure 4 – A Rubik’s cube and its perimeter in 3D.

Solution

We can see (from figure 4) a total of eight corner vertices and six faces on the Rubik’s cube. These corner vertices are A, B, C, D, E, F, G, and H. The six faces are then:

1. ABFE: Front
2. CDHG: Back
3. BCGF: Right
4. DAEH: Left
5. EFGH: Top
6. ABCD: Bottom

Two faces are adjacent when they share at least one vertex. With this logic, we can see that the adjacent faces and the common vertices are:

1. Front and Right (ABFE and BCGF): B + F
2. Front and Left (BFE and DAEH): A + E
3. Front and Top (ABFE and EFGH): E + F
4. Front and Bottom (ABFE and ABCD): A + B
5. Back and Right (CDHG and BCGF): C + G
6. Back and Left (CDHG and DAEH): D + H
7. Back and Top (CDHG and EFGH): G + H
8. Back and Bottom (CDHG and ABCD): C + D
9. Right and Top (BCGF and EFGH): F + G
10. Right and Bottom (BCGF and ABCD): B + C
11. Left and Top (DAEH and EFGH): E + H
12. Left and Bottom (DAEH and ABCD): A + D

So there are a total of 12 adjacent face pairs in a cube. We can do the same for each side of the cube as well!

All mathematical drawings and images were created with GeoGebra.

Adjacent Side Triangle Definition < Glossary Index > Algebra Definition